In this post we'll meet a staple at the Differential Geometry math art shop: Flat tori in four-space, and "conformal torus knots" lying on these surfaces. Although we generally strive in these posts to avoid coordinates, we'll refer to Cartesian coordinates throughout.
Our story starts with circles in the plane. If \(t\) is real, the point \(c(t) = (\cos t, \sin t)\) lies on the unit circle in the Cartesian plane, and the ray from the origin to \(c(t)\) makes a counterclockwise angle \(t\) measured from the rightward-pointing horizontal. As \(t\) runs from \(0\) to \(2\pi\), this point traces the unit circle once counterclockwise.
With small modifications to this expression, we can trace a circle of chosen positive radius \(r\) and speed \(k\): \[ c_{r}(kt) = (r\cos kt, r\sin kt). \] For each real \(t\), this point lies on the circle of radius \(r\) centered at the origin, and makes polar angle \(kt\) relative to the rightward-pointing horizontal. As \(t\) runs from \(0\) to \(2\pi\), this point traces the circle \(|k|\) times: counterclockwise if \(k\) is positive and clockwise if \(k\) is negative.
Our blog post on compound circular motion describes ways we can combine circular motions in the plane to get more complicated shapes than circles.
Our strategy here is algebraically simpler but geometrically less intuitive: We'll concatenate expressions, obtaining descriptions of curves and surfaces in four-space! Specifically, if \(a\) and \(b\) are positive real numbers and if \(u\) and \(v\) are real parameters (numbers that vary freely), we'll consider points of the form \[ C_{a,b}(u, v) = (a\cos u, a\sin u, b\cos v, b\sin v). \]
How might we conceptualize, much less visualize, a set of points in four-space? Our post on High-Dimensional Geometry gives generalities. Here we have a specific example, and might hope for more detailed pictures.
An object in four-space can be "projected" to a lower dimensional space by discarding one or more coordinates. The effect is similar to the shadow of a spatial object cast by a point light source placed very far away, so the incident rays are nearly parallel. Indeed, if \((x, y, z)\) is a point of three-space, then \((x, y)\) is the shadow cast by a light source far along the \(z\)-axis if we identify the Cartesian plane with the set of points with coordinates \((x, y, 0)\); in the same way, \((x, z)\) is the shadow cast by a light source far along the \(y\)-axis, and \((y, z)\) is the shadow cast by a light source far along the \(x\)-axis.
Discarding the third and fourth coordinates gives the set of pairs \((a\cos u, a\sin u)\), which we recognize as the circle of radius \(a\) about the origin, traced counterclockwise. The set of all points \(C_{a, b}(u, v)\) casts the circle of radius \(a\) as planar shadow, comparably to a cylindrical cardboard tube seen from a point along its axis.
Similarly, discarding the first and second coordinates gives the set of pairs \((b\cos v, b\sin v)\), which we recognize as the circle of radius \(b\) about the origin, traced counterclockwise.
If \(a\) and \(b\) are fixed, the set of all points \[ C_{a,b}(u, v) = (a\cos u, a\sin u, b\cos v, b\sin v) \] is a surface that casts circular shadows in two perpendicular coordinate planes. These circles are "independent" in the same way two axes of a rectangle are independent: for each point on one circle, the object contains all the points on the other circle, and no others. Mathematically, this shape is a Cartesian product of circles.
Think of an idealized donut or bagel with a hole. Each half-plane bordered by the axis cuts the pastry in a longitude circle (gold). Further, if we pick an arbitrary point on a longitude circle and sweep it around the axis, we get a latitude circle (blue). Finally, the surface of the pastry is the totality of the latitude circles. In other words, a point on our pastry lies on precisely one longitude and one latitude. Abstractly, our pastry is a Cartesian product of circles. In other words, a Cartesian product of two circles is a torus.
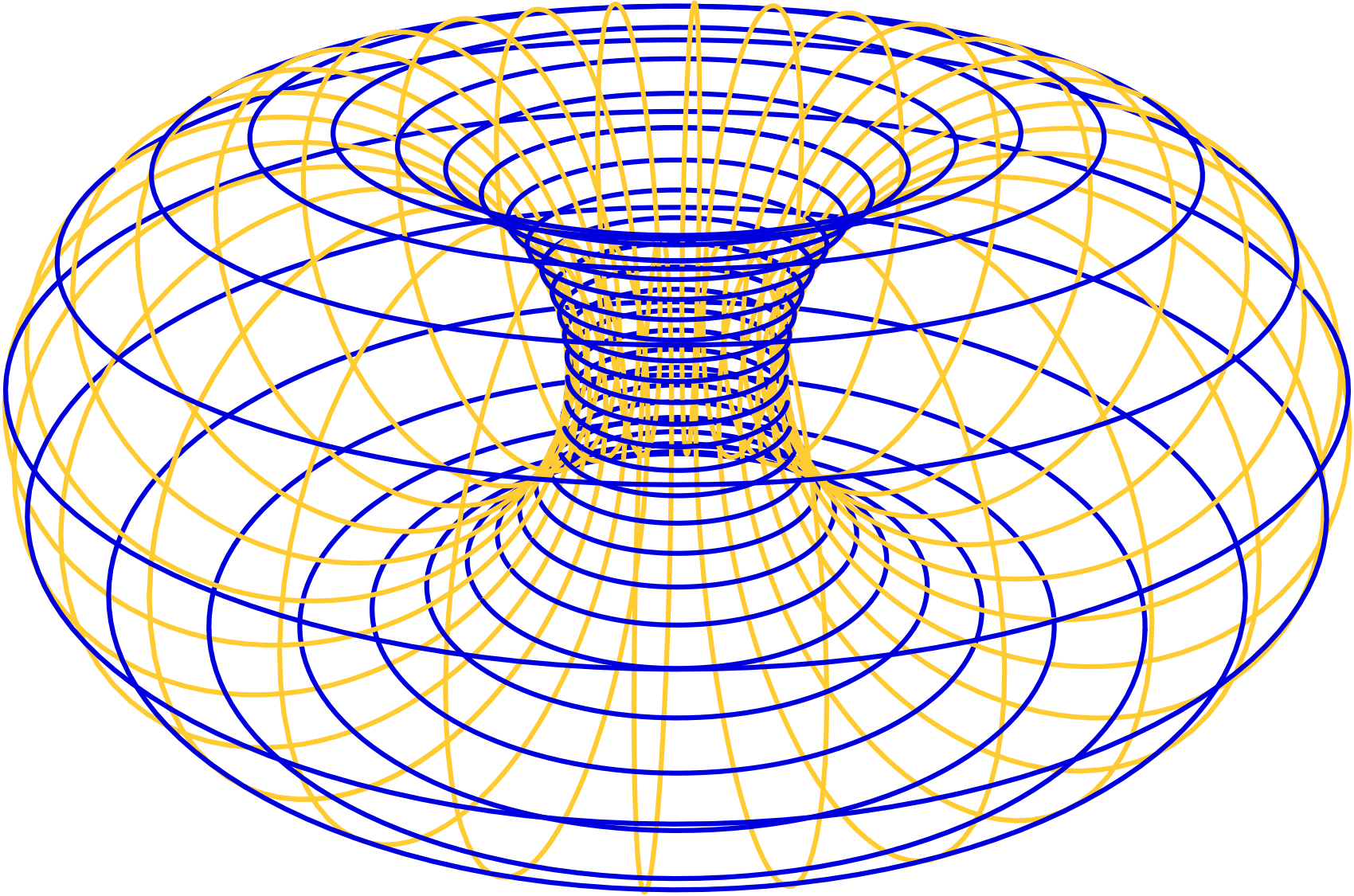
Unlike a familiar torus in three-space, a Cartesian product of circles in four-space is "flat" or "has Euclidean geometry." If we start with a \(2\pi a \times 2\pi b\) rectangle we can wrap one direction around a circle of radius \(a\) without crinkling or tearing, obtaining an ordinary cylinder. In three-space there is no way to roll the cylinder into a torus without crinkling or tearing, but in four-space the second axis can be rolled just as easily as the first. We'll call a Cartesian product of circles a Clifford torus, after English mathematician William Kingdon Clifford.
A Clifford torus lies on a sphere in four-space centered at the origin: The distance from the origin \((0, 0, 0, 0)\) to the point \[ (x, y, z, w) = C_{a, b}(u, v) = (a\cos u, a\sin u, b\cos v, b\sin v) \] is \begin{align*} \sqrt{x^{2} + y^{2} + z^{2} + w^{2}} &= \sqrt{(a\cos u)^{2} + (a\sin u)^{2} + (b\cos v)^{2} + (b\sin v)^{2}} \\ &= \sqrt{a^{2}(\cos^{2} u + \sin^{2} u) + b^{2}(\cos^{2} v + \sin^{2} v)} \\ &= \sqrt{a^{2} + b^{2}}. \end{align*} This does not depend on \(u\) or \(v\), so is constant over the torus.
We'd like to visualize a Clifford torus with more subtlety than our plane projections. One pleasant method is to scale our Clifford torus to lie in the unit sphere in four-space, then map the unit sphere to three-space by stereographic projection from \((0, 0, 0, 1)\). Algebraically, we assume \(a^{2} + b^{2} = 1\), and map \[ (x, y, z, w) = C_{a, b}(u, v) = (a\cos u, a\sin u, b\cos v, b\sin v) \] to \[ \frac{1}{1 - w}(x, y, z) = \frac{1}{1 - b\sin v}(a\cos u, a\sin u, b\cos v). \] Because the "parametrization" \(C_{a, b}\) preserves lengths and angles, and separately stereographic projection preserves angles, the preceding parametrization of the torus also preserves angles, or is conformal. Particularly, if two curves meet perpendicularly in the plane, their images on the torus meet perpendicularly.
The interactive program Torus Sketch lets you draw in the plane and map what you draw in real time to the Clifford torus with \(a = b\). The \((u, v)\)-plane can be shifted left-right and up-down, which moves the image curves correspondingly.
What happens to a line in the plane under our conformal parametrization of a torus? If the line is horizontal (\(v\) is constant), it maps to a circle about the \(z\)-axis of radius \(a/(1 - b\sin v)\) and height \(b\cos v/(1 - b\sin v)\), a latitude of our torus. If the line is vertical (\(u\) is constant), it maps to a longitude circle, but the center and radius are not so easily read off the formula.
What about a line of slope \(1\)? In the \((u, v)\)-plane, let's first consider the line \(v = u\). The path traced in the three-sphere is \[ (a\cos u, a\sin u, b\cos u, b\sin u) = (a, 0, b, 0)\cos u + (0, a, 0, b) \sin u. \] The vectors \((a, 0, b, 0)\) and \((0, a, 0, b)\) each have length \(1\), and they are mutually perpendicular. The preceding "trigonometric linear combination" consequently traces a circle of radius \(1\), i.e., a great circle in the three-sphere. With a bit more calculation involving trig identities, we similarly deduce that every line of slope \(1\) maps to a great circle. The same is true for lines of slope \(-1\). It turns out, further, that stereographic projection maps circles in the three-sphere to circles or lines in three-space. In summary, a line of slope \(\pm 1\) in the \((u, v)\) plane maps to a circle in three-space. These curves are called Villarceau circles on the torus, after French mathematician Yvon Villarceau.
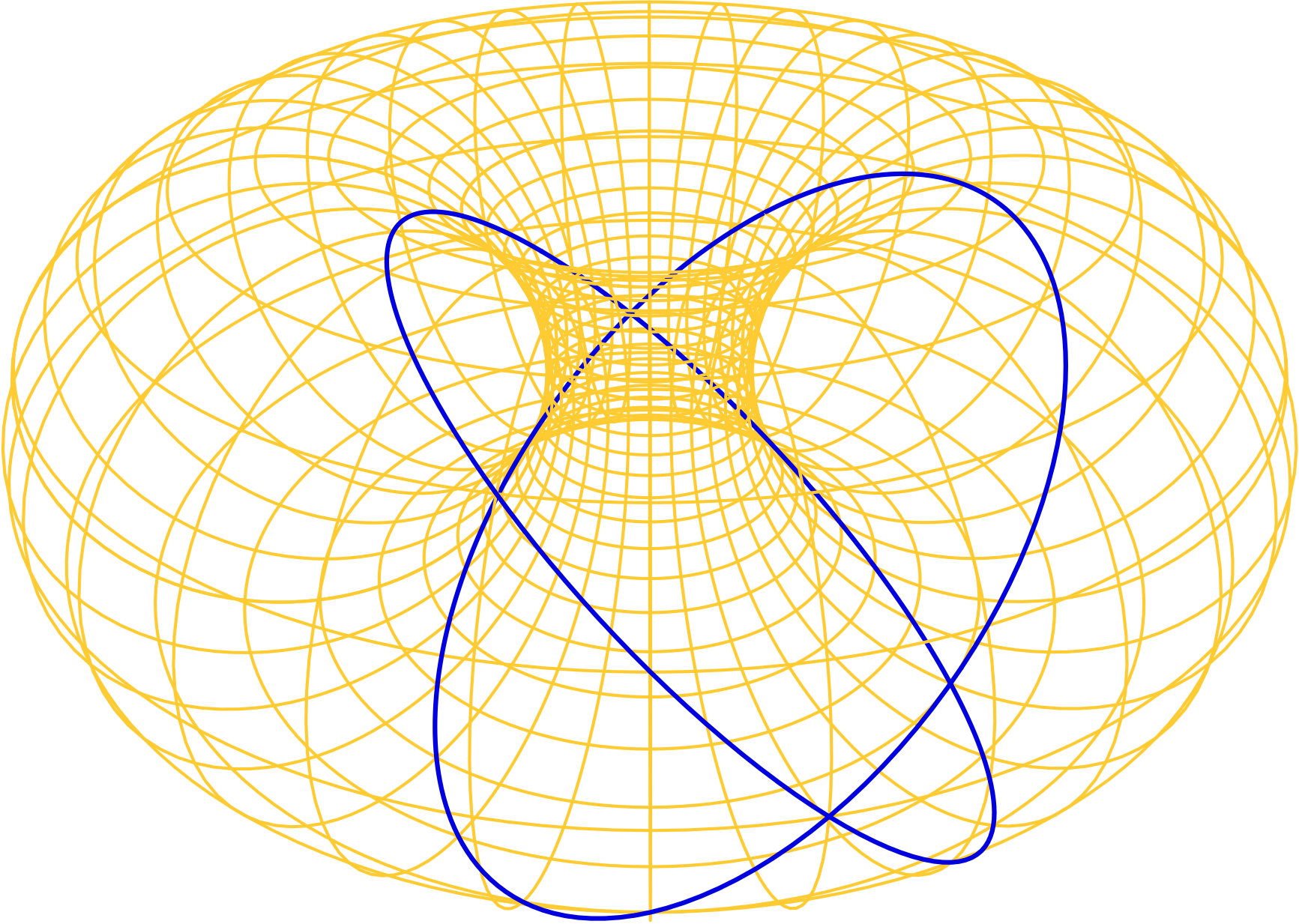
Cyclide-based jewelry designs at the Differential Geometry math art shop, including Selene and Celeste earrings, and the Luna pendant, are based upon Villarceau circles.
What about lines other than horizontal, vertical, or diagonal of slope \(\pm1\)? Although these curves are not circles, they too possess a distinctive elegance, and inspire jewelry designs including Intimo (slope \(\frac{2}{3}\), described by setting \(v = \frac{2}{3}u\) in the Clifford torus, i.e., as the set of points \((a\cos 3t, a\sin 3t, b\cos 2t, b\sin 2t)\) for \(t\) real) and Harmonia (slope \(\frac{5}{6}\), similarly described as the set of points \((a\cos 6t, a\sin 6t, b\cos 5t, b\sin 5t)\) for \(t\) real). Generally, such a curve is closed precisely when its slope is rational (a ratio of integers). If the slope is rational but neither an integer nor the reciprocal of an integer, the curve in three-space is knotted.
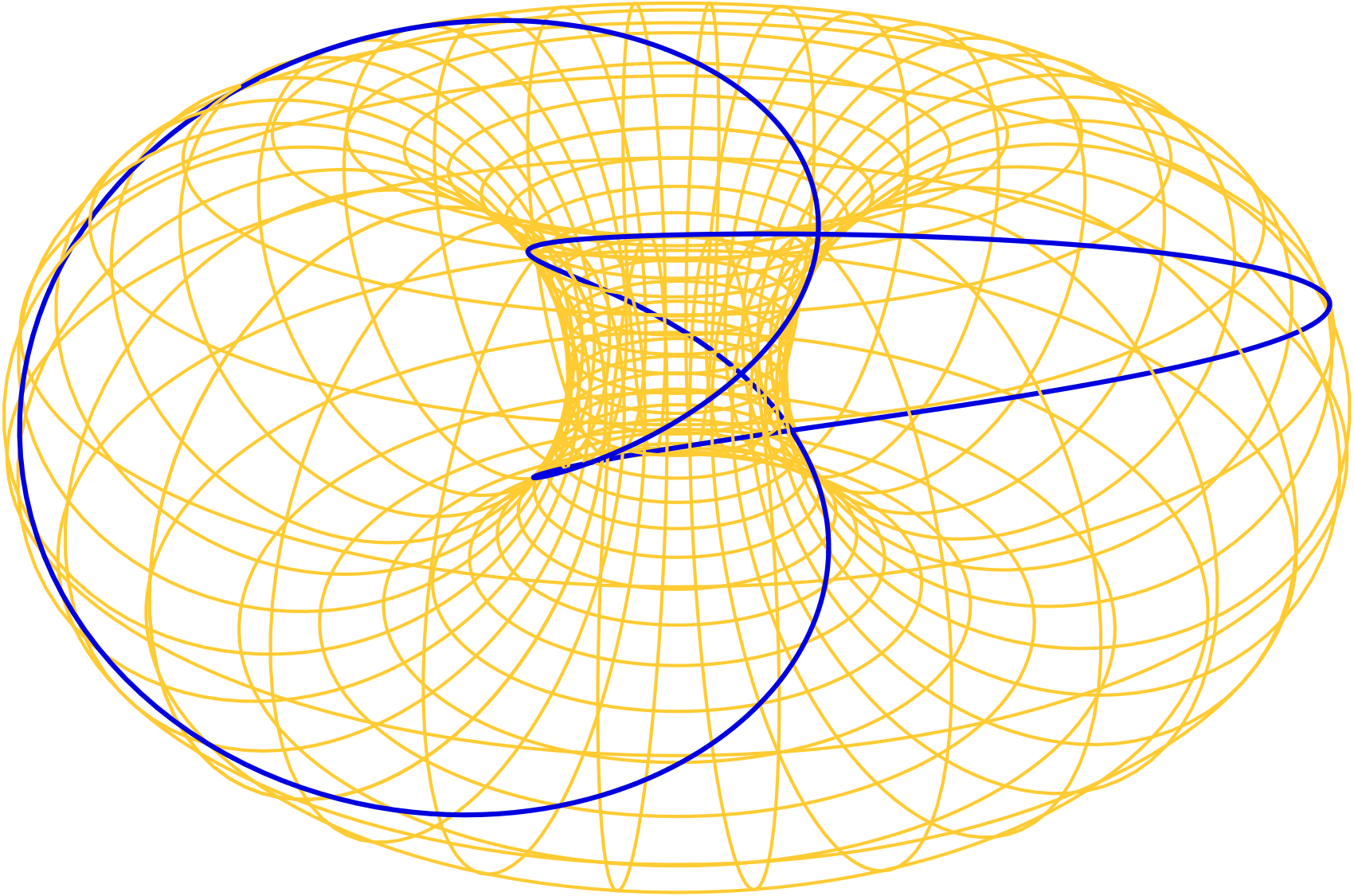
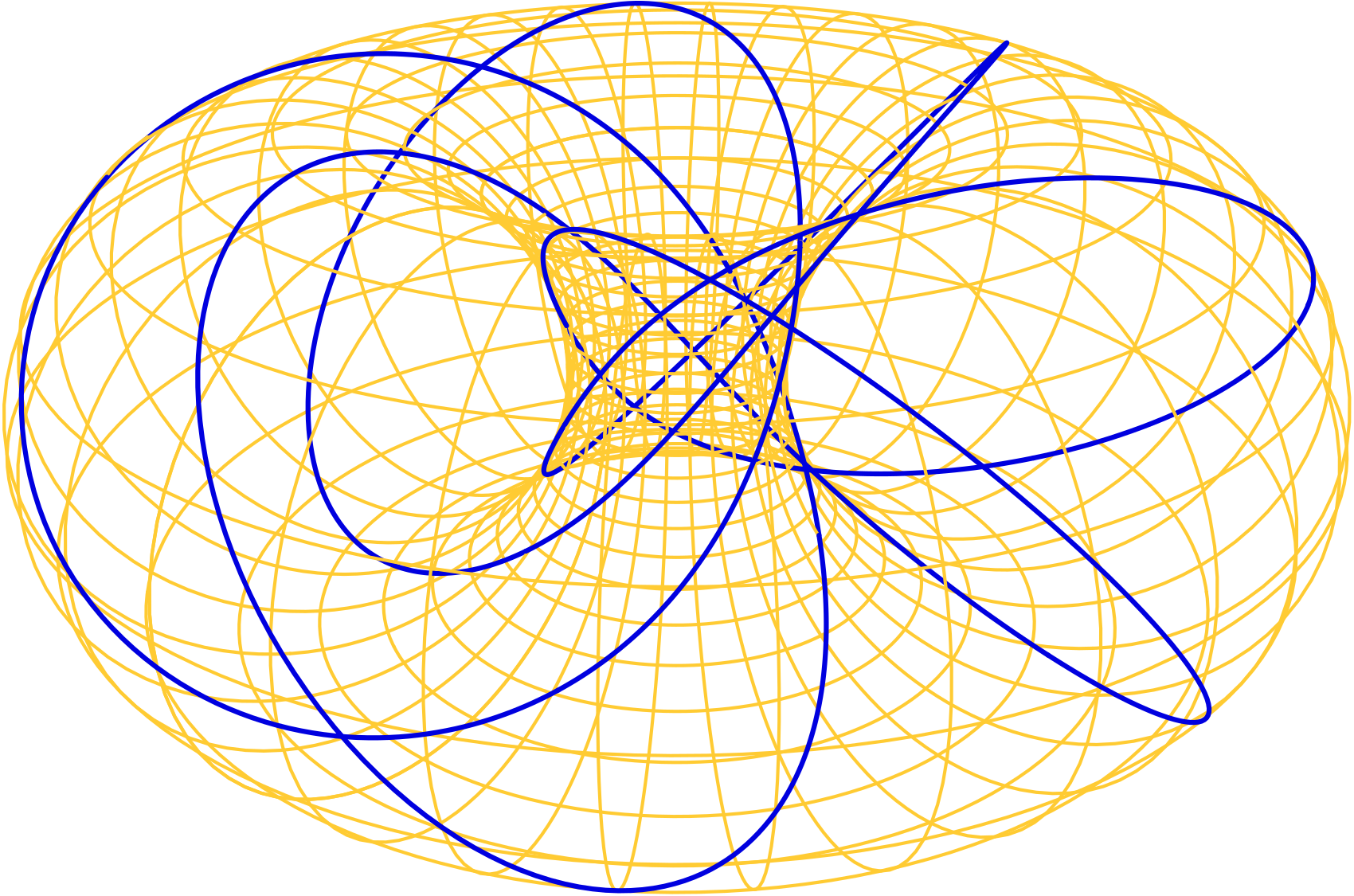
To finish, here are some provocative mathematical thoughts. Our jewelry pieces inspired by complex vectors and circles can be represented concretely as physical objects. To find them, however, and to describe them simply, entailed passing through Euclidean four-space.
Does four-space "exist"? If so, where is it? If not, why does manipulating four-tuples of numbers as if they were spatial coordinates lead to such compelling shapes, to plausible analogies with three-dimensional intuition?