Compound Circular Motion

Circles and Parametrization

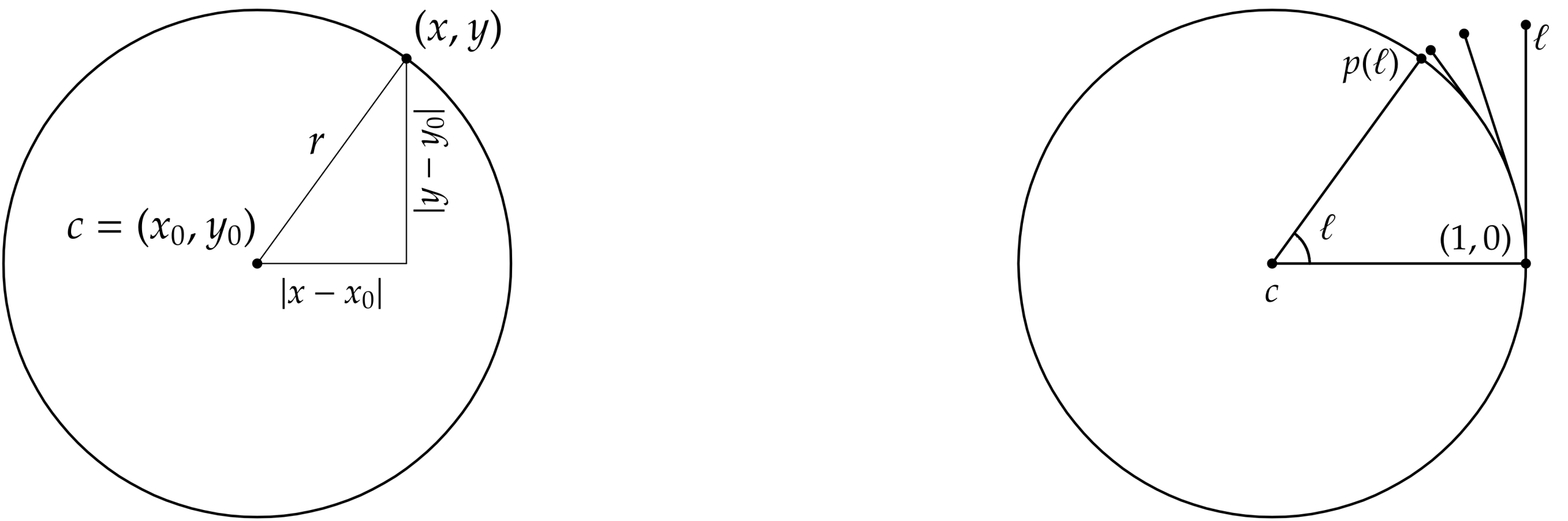
Recall that a circle is the set of points in a plane lying at fixed radius \(r\) from a point, the center. In Cartesian coordinates, if \(c = (x_{0}, y_{0})\) is the center, then a point \((x, y)\) lies on the circle of radius \(r\) about \(c\) precisely when \[ (x - x_{0})^{2} + (y - y_{0})^{2} = r^{2}. \] This equation looks intimidating, but merely expresses the familiar Pythagorean theorem.

A circle is a set of points in the plane. For our purposes, it is easier to work with a way of describing how a circle is traced by a moving point as a function of a "parameter" \(t\).

To a mathematician, generally, a curve is a set of points, while a path is a mapping that describes how a curve is traced by a moving point. In mathematics, the terms "curve" and "path" are not interchangeable. A curve is what we see drawn on a page or screen. A path is a particular manner we draw a curve.

The prototypical circle path comes from trigonometry. Recall that if \(\theta\) is a real number, there is an angle \(\theta\) measured counterclockwise from the positive horizontal axis, and the point on the unit circle at angle \(\theta\) has Cartesian coordinates \((\cos\theta, \sin\theta)\). If we let angle be our parameter, namely if we set \(\theta = t\), the function \[ c(t) = (\cos t, \sin t) \] traces the unit circle when \(t\) runs over any real interval of length \(2\pi\). A common choice of interval is \([0, 2\pi]\). When \(t = 0\), we have \(c(t) = c(0) = (\cos 0, \sin 0) = (1, 0)\). When \(t = 2\pi\), we similarly have \(c(t) = (1, 0)\). For values of \(t\) between \(0\) and \(2\pi\), \(c(t)\) is some other point of the unit circle. Further, every point of the circle except \((1, 0)\) occurs precisely once.

Here are a few exercises to ponder, whose answers may be found below.

1. The most general real interval of length \(2\pi\) may be written \([\theta_{0}, \theta_{0} + 2\pi]\) for some real number \(\theta_{0}\) (read theta naught, and signifying an "initial value" of \(\theta\)). How does the point \(c(t)\) move if \(t\) runs over this interval? Particularly, where does the point start and finish?
2. How can we describe the motion of a point that traces only part of the circle, or traces the circle multiple times?
3. The circles we have seen so far travel at unit speed, and travel a distance \(2\pi\), the circumference of the unit circle, in "time" \(2\pi\). How could we make our particle travel twice as fast, so the entire circle is traced as \(t\) moves over an interval of length \(\pi\)? Three times as fast? Half as fast? (Hint: Think about scaling \(t\).)
4. How could we make our particle trace a circle of radius \(2\)? (Hint: Think about scaling the plane coordinates \(x\) and \(y\). It may help to review complex numbers.)
5. How could we make our particle trace a circle of radius \(1\) centered at \((-4, 3)\) instead of at the origin? (Hint: Think of using vector addition to shift.)

The animation shows nine paths (three radii, three angular speeds) tracing three circles. The colors green, red, and blue signify "small" (radius and speed), "medium," and "large."

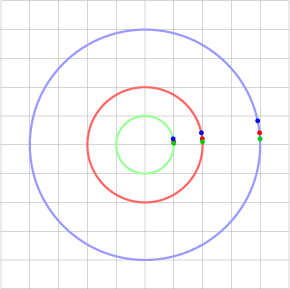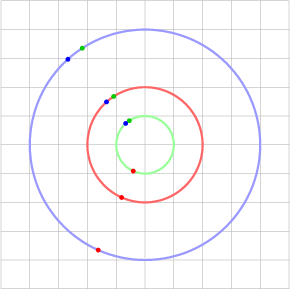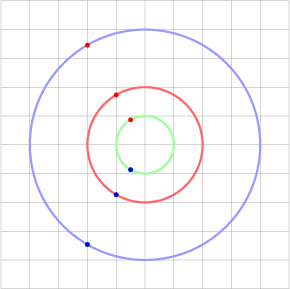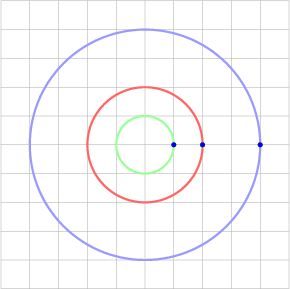
Let's consider the preceding questions one at a time.

1. If we shift our parameter interval to \([\theta_{0}, \theta_{0} + 2\pi]\), keeping the length as \(2\pi\), our particle traces the circle one full turn counterclockwise, but starts and ends at the point \(c(\theta_{0})\). For example, the parameter interval \([-\pi, \pi]\) gives a particle that starts and ends at \(c(-\pi) = c(\pi) = (-1, 0)\).
2. To trace the portion of the unit circle in the first quadrant, we can use the same formula \(c(t) = (\cos t, \sin t)\) but change the parameter interval to \([0, \frac{\pi}{2}]\). Our path starts at \(c(0) = (1, 0)\) and ends at \(c(\frac{\pi}{2}) = (0, 1)\).
   To trace the unit circle three times, we can similarly change our parameter interval to \([0, 6\pi]\). Our path starts and ends at \(c(0) = c(6\pi) = (1, 0)\), but traverses the circle once each time \(t\) advances by \(2\pi\). Since our interval has length \(6\pi = 3 \times 2\pi\), the circle is traced three times.
   Generally, changing the endpoints of our parameter interval changes the starting and final points of our path: If \(t_{0}\) is our initial parameter value and \(t_{1}\) is our final value, then letting \(t\) run over the interval \([t_{0}, t_{1}]\) gives a path starting at \(c(t_{0})\), ending at \(c(t_{1})\), and wrapping around the circle as dictated by the length of the interval.
3. Consider the path \(c_{2}(t) = c(2t) = (\cos 2t, \sin 2t)\), which we may view as taking \(\theta = 2t\). When \(t\) advances by \(2\pi\), the angle \(\theta\) advances by twice as much: \(4\pi\). Geometrically, this corresponds to a point moving two full turns around the unit circle. Dynamically, multiplying the parameter \(t\) by \(2\) "makes the path run twice as fast."
   Similarly, the path \(c_{3}(t) = c(3t)\) traces the circle three times as fast as \(c\), completing one full turn on an interval of length \(\frac{2}{3}\pi\).
   To slow our path, we can scale time by \(\frac{1}{2}\), yielding \(c_{1/2}(t) = c(t/2) = \bigl(\cos(t/2), \sin(t/2)\bigr)\).
4. To trace a circle of radius \(2\), it suffices to scale each component of our path. Thus, we might define \(C_{2}(t) = 2c(t) = (2\cos t, 2\sin t)\). This path moves counterclockwise around the circle of radius \(2\) centered at the origin, and completes one full turn on an interval of length \(2\pi\).
   To trace the circle of arbitrary radius \(r\) about the origin, we may use the path \(C_{r}(t) = (r\cos t, r\sin t)\).
5. To trace the circle of radius \(1\) and center \((-4, 3)\), it suffices to add the center and our path \(c(t)\) componentwise, obtaining \(C(t) = (-4 + \cos t, 3 + \sin t)\).

In practice, we often need to combine all these operations in one formula. Suppose our circle is to have radius \(r\) and center \((x_{0}, y_{0})\), and is to complete one full turn counterclockwise in time \(2\pi/\omega\) for some non-zero frequency \(\omega\). The path \begin{align*} c(t) &= (x_{0}, y_{0}) + r\bigl(\cos(\omega t), \sin(\omega t)\bigr) \\ &= \bigl(x_{0} + r\cos(\omega t), y_{0} + r\sin(\omega t)\bigr) \end{align*} accomplishes the task. When the frequency \(\omega\) is negative, the point moves clockwise.

Epicycles

Equipped with the tool of circle parametrizations, we can have a lot of fun with paths! As proof of concept, let's imagine a point \(p\) moving at unit speed along the unit circle, and further imagine a point \(q\) moving in a circle around \(p\) with some radius \(r\) and frequency \(\omega\). This is, in modern guise, how Johannes Kepler attempted to describe the motions of planets about the sun.

The motion of \(p\) relative to the origin is described by the path \((\cos t, \sin t)\).

The motion of \(q\) relative to \(p\) is described by the path \(\bigl(r\cos(\omega t), r\sin(\omega t)\bigr)\).

The combined motion is the vector sum: \begin{align*} c(t) &= \bigl(\cos t, \sin t\bigr) + \bigl(r\cos(\omega t) + r\sin(\omega t)\bigr) \\ &= \bigl(\cos t + r\cos(\omega t), \sin t + r\sin(\omega t)\bigr). \end{align*} Given the ease of writing this path, it may be a surprise that finding an equation for the curve traced is difficult. Particularly, if \(\omega\) is not a ratio of whole numbers, this path is not periodic. Loosely, the path never returns to its initial position and velocity.

The epicycles shown each have five-fold symmetry. Close inspection reveals that the blue segment rotates counterclockwise four times relative to horizontal while the red segment rotates clockwise six times. The counterclockwise motion of the center affects clockwise and counterclockwise "orbital motion" differently. This effect will be important when we roll one circle inside another.

The tips of the arrowheads in our topological index poster trace the epicycles \[ c(t) = (\cos t, \sin t) + \tfrac{1}{4}(\cos kt, \sin kt) \] for \(k\) a non-zero whole number between \(-4\) and \(4\).

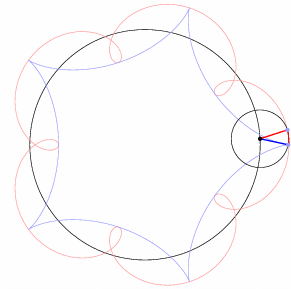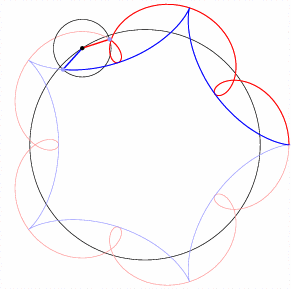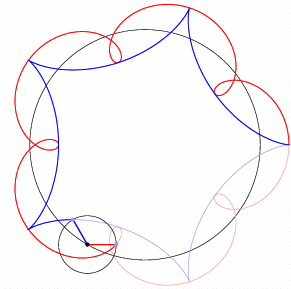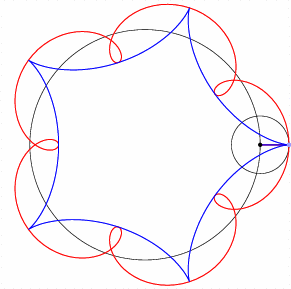
We can construct ever-more-complicated paths by imagining a third point revolving about \(q\), and so forth. An interactive calculator such as Desmos is useful for experimenting!

Rolling

As a special case of epicycles, let's investigate how one circle might roll along another curve, either a line or a circle, without slipping.

Cycloids

Suppose a circle of radius \(R\) rolls to the right without slipping, at horizontal speed \(v\) along the \(x\)-axis. Our goal is to describe the motions of points on the circumference.

If the circle is centered on the vertical axis at time \(t = 0\), then the center of the circle is given by the path \((vt, R)\). It suffices to determine the position of a point on the circle relative to the center, and to take the vector sum.

We'll first calculate the frequency. When the circle has made one full turn, the center has moved to the point \((vt, R) = (2\pi R, R)\). Equating the first components and solving for \(t\) tells us the circle makes one full turn between \(t = 0\) and \(t = 2\pi R/v\). But in terms of frequency, the time for one full turn is \(2\pi/\omega\). Setting \(2\pi R/v = 2\pi/\omega\) and solving gives \(\omega = v/R\).

Because the circle rotates clockwise relative to the center, the frequency is negative. If our point \(q\) is initially at location \((0, -R)\) relative to the center, i.e., is initially directly below the center (on the horizontal axis) at angle \(\theta_{0} = -\frac{\pi}{2}\), its motion relative to the center is described by \[ \bigl(R\cos(\tfrac{\pi}{2} - vt/R), R\sin(\tfrac{\pi}{2} - vt/R)\bigr) = \bigl(-R\sin(vt/R), -R\cos(vt/R)\bigr). \] The net motion of our point on the circumference is \[ c(t) = (vt, R) - \bigl(R\sin(vt/R), R\cos(vt/R)\bigr) = \bigl(vt - R\sin(vt/R), R - R\cos(vt/R)\bigr). \] The curve traced is called a cycloid.

By similar reasoning, we can deduce the motion of an arbitrary point on or inside the circle: If the point's initial position is \((-r\sin\theta_{0}, R - r\cos\theta_{0})\), its motion is given by \[ c(t) = \bigl(vt - r\sin(\theta_{0} + vt/R), R - r\cos(\theta_{0} + vt/R)\bigr). \] This formula is correct even if \(R < r\), i.e., the point is "outside" the rolling circle, like a point on the flange of a train wheel. Using calculus, one can show that for a small portion of each turn, points on the flange move backward relative to the ground!

Hypocycloids

One final application gives mathematics behind the toy Spirograph. Mathematically, we have a ring of inner radius \(R\) and a gear of radius \(r < R\) that rolls inside the ring without slipping. The gear has holes through which a pen fits. By rolling the gear inside the ring, we draw striking patterns whose symmetry depends on the ratio \(r/R\).

Before (or after) reading further, you may enjoy this interactive drawing program. Hover the cursor over the gear to preview the pattern, and click to draw. The pen color, and the sizes of the ring and gear may be set. You can draw multiple patterns, perform limited editing (removal of paths already drawn), and same your picture as a png file.

Abstractly, the analysis matches our reasoning for cycloids. First, the center of the gear moves along a circle of radius \(R - r\), so the center of the gear is described by \[ c_{0}(t) = (R - r)(\cos t, \sin t). \] It remains to describe the motion of points of the gear relative to the center of the gear.

Consider an inward-pointing unit vector \(e\) along the ring. The circumference of the ring is \(2\pi R\), the circumference of the gear is \(2\pi r\). As the gear rolls all the way (one full turn) around the ring, it rotates through \((2\pi R)/(2\pi r) = R/r\) full turns clockwise relative to \(e\).

But \(e\) itself rotates one full turn counterclockwise relative to a rightward-pointing vector along the ring. The gear therefore rotates clockwise through \((R/r) - 1 = (R - r)/r\) full turns relative to the Cartesian directions. Equivalently, the gear rotates counter-clockwise through \(1 - (R/r) = (r - R)/r\) full turns relative to the Cartesian directions.

The motion of a point on the rim of the gear relative to the center is therefore \[ c_{1}(t) = r\bigl(\cos\tfrac{r - R}{r}t, \sin\tfrac{r - R}{r}t\bigr). \] Combining with the circular motion of the center of the gear gives the hypocycloid path \[ c(t) = (R - r)(\cos t, \sin t) + r\bigl(\cos\tfrac{r - R}{r}t, \sin\tfrac{r - R}{r}t\bigr). \]

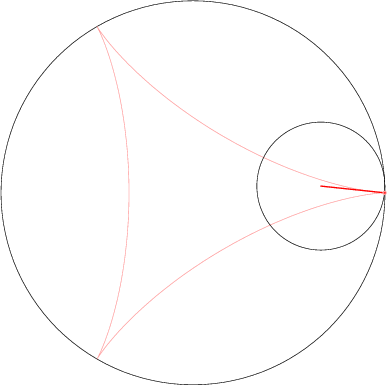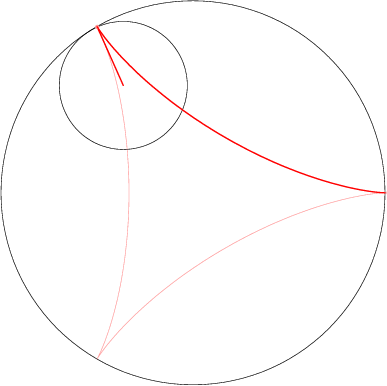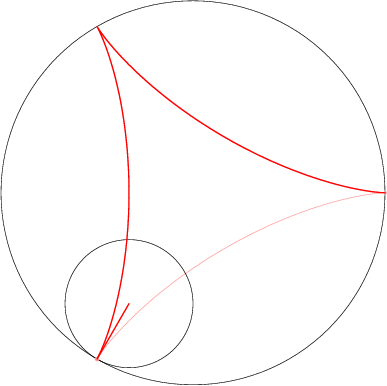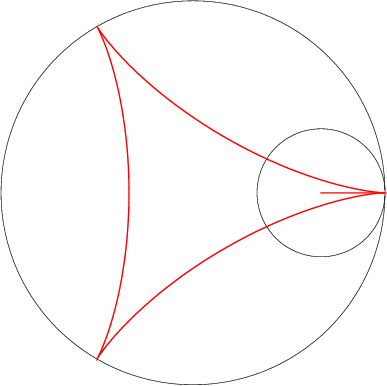
Specifically, this path describes the motion of the rightmost point of the gear then the gear is rightmost inside the ring. To follow the point with polar coordinates \((r_{0}, \theta_{0})\) relative to the center of the gear when the gear is rightmost, we need only modify in the second summand the polar radius and the angle inside the trig functions. Writing \(\theta(t) = \theta_{0} + \frac{r - R}{r}t\) for simplicity, we obtain the path \[ c(t) = (R - r)(\cos t, \sin t) + r_{0}\bigl(\cos \theta(t), \sin \theta(t)\bigr). \] As with the cycloid, this formula is correct even for points outside the gear, with \(r < r_{0}\).

You may enjoy deducing the corresponding formula for a gear rolling on the outside of a circular ring. An answer is given below.

Summary

Circular motion at constant speed is straightforward to describe with a path whose components are trig functions. This simplicity is deceptive, however. By "superposing" circular motion on circular motion, we obtain visually appealing paths whose behavior is far from simple.

For algebra purposes, the formalism of complex numbers often provides valuable simplification. Recall that for all real \(\theta\), \[ e^{i\theta} = \cos\theta + i\sin\theta. \] If we write \(\omega = (r - R)/r\), the hypocycloid formula becomes \[ c(t) = (R - r)e^{it} + r_{0}e^{i\omega t + \theta_{0}}. \] We can now easily factor out \(e^{it}\) and (assuming \(\omega\) is rational) use algebra to investigate the symmetry of the curve traced.

These ideas about circular motion extend easily to paths in three-space and higher dimensions. Many images and objects at the Differential Geometry math art shop are shadows of paths in four- or six-space obtained by superposing different uniform circular motions.

Answer: The hypocycloid obtained by rolling a gear outside the ring needs two modifications from the discussion above. First, the center of the gear moves on a circle of radius \(R + r\) rather than \(R - r\). Second, the gear turns counterclockwise rather than clockwise. If we write \(\theta(t) = \theta_{0} + \frac{R + r}{r} t\), the resulting path is \[ c(t) = (R + r)(\cos t, \sin t) + r_{0}\bigl(\cos \theta(t), \sin \theta(t)\bigr). \]