“Point projection” is a simple model for representing a three-dimensional scene on a planar canvas in perspective. Fix a plane \(P\) in three-space and a point \(p\) not on \(P\). For each point \(x\) distinct from \(p\), there is a unique line through \(p\) and \(x\). If this line is not parallel to \(P\), it intersects \(P\) in a unique point, which we’ll denote \(\Pi(x)\).
If we view \(p\) as a point light source and \(x\) as the location of an object, we may view \(\Pi(x)\) as the location of the shadow of \(x\) on the plane \(P\). This rule defines a mapping \(\Pi\), called point projection from \(p\) onto \(P\), from “most” points of space to the plane \(P\). This mapping is undefined on points of the plane through \(p\) and parallel to \(P\).
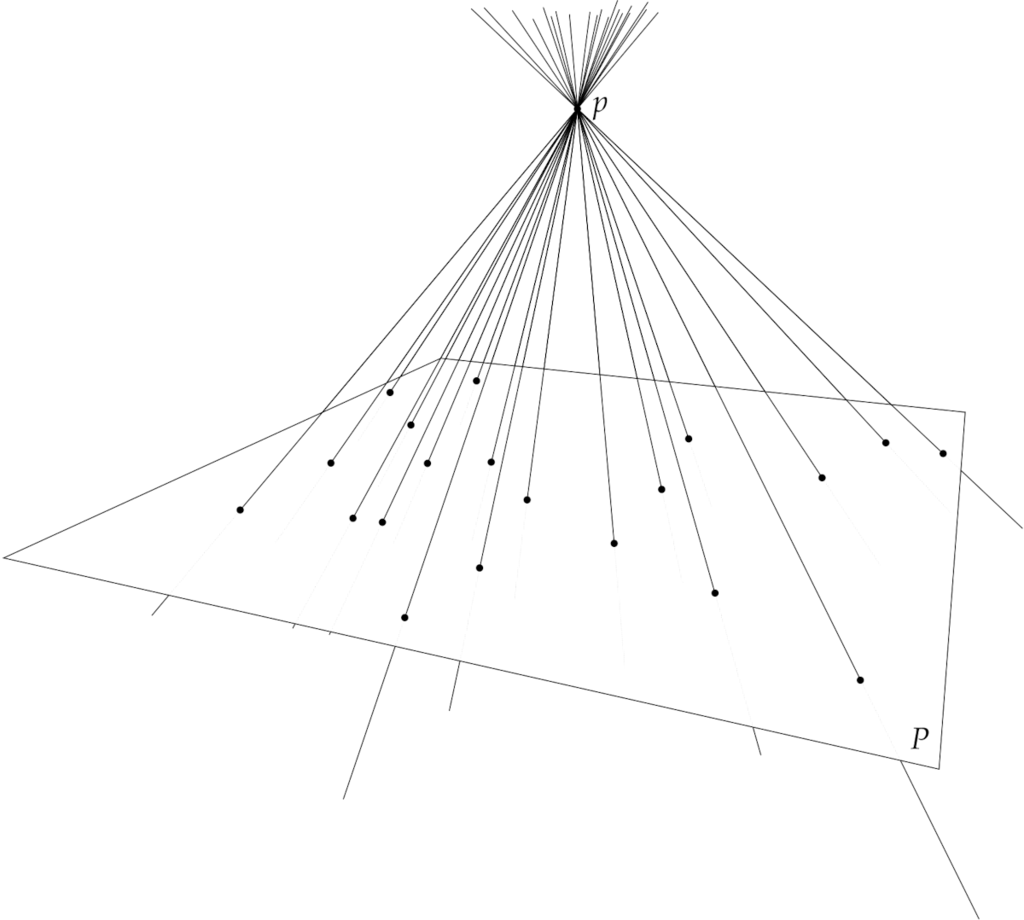
Alternatively, if we view \(p\) as the location of an eye and \(P\) as a screen, then the points at spatial location \(x\) and \(\Pi(x)\) appear to be at the same place to the eye. In this way, point projection represents spatial scenes in the plane \(P\).
Point projection may be easier to view “in reverse”: For each point \(q\) of \(P\), there is a unique line \(L\) through \(q\) and \(p\). The points of \(L\) are precisely those that map to \(q\) under the projection \(\Pi\).
Stereographic Projection
Place a sphere \(S\) in space passing through the light source \(p\) so that the plane tangent to \(S\) at \(p\) is parallel to \(P\). Every line through \(p\) and a point of \(S\) hits the plane \(P\) in a unique point. Conversely, each point of \(P\) determines with \(p\) a unique line, and this line hits \(S\) at two distinct points, one of them \(p\) itself.
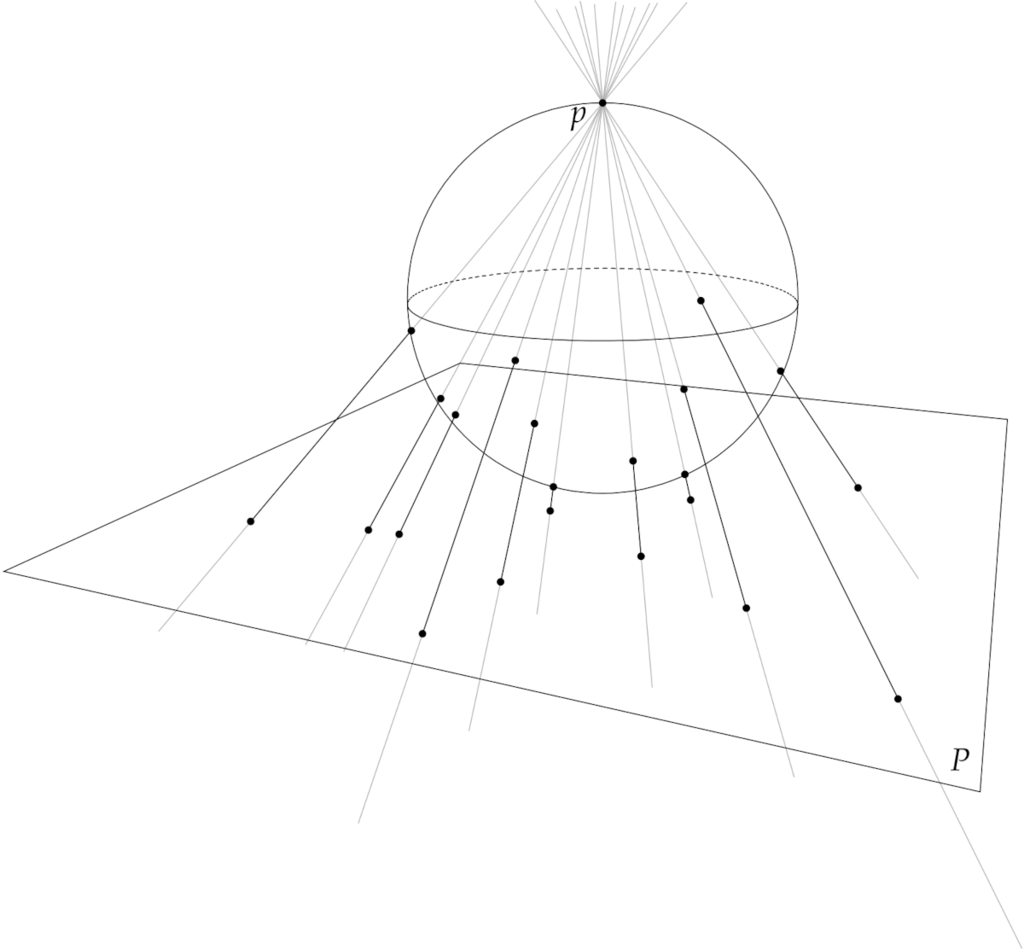
In other words, using point projection from \(p\) we have set up a dictionary between points of \(P\) and points of \(S\) other than \(p\). This mapping from the “punctured sphere” (\(S\) with \(p\) removed) to the plane \(P\) is known as stereographic projection (of \(S\)) from \(p\). In geographic terms, we may represent on a single infinite map the surface of a globe with one point removed. In practice the north pole of the earth is removed. Further, since a paper map has finite size, a stereographic map necessarily omits part of the arctic region.
If we travel along a line in \(P\), our “corresponding” point on the sphere approaches the light source \(p\). We may interpret this geometric fact by saying stereographic projection from \(p\) allows us to view the sphere \(S\) as the plane \(P\) with one point at infinity. Talk of “infinity” requires care, but stereographic projection illustrates mathematical benefits of treating infinity concretely, of choosing to visualize a single point at infinity “in a plane” as a specific location on a sphere.
It will be convenient to view a line in the plane as a “circle of infinite radius.” This is less mystical that it may sound. A large circle, such as the equator if the earth were a perfect sphere, looks to the eye like a line. The family of circles in the plane with center \((0, r)\) and radius \(r\), as \(r\) ranges over the positive real numbers, appears to contain the horizontal axis, a line.
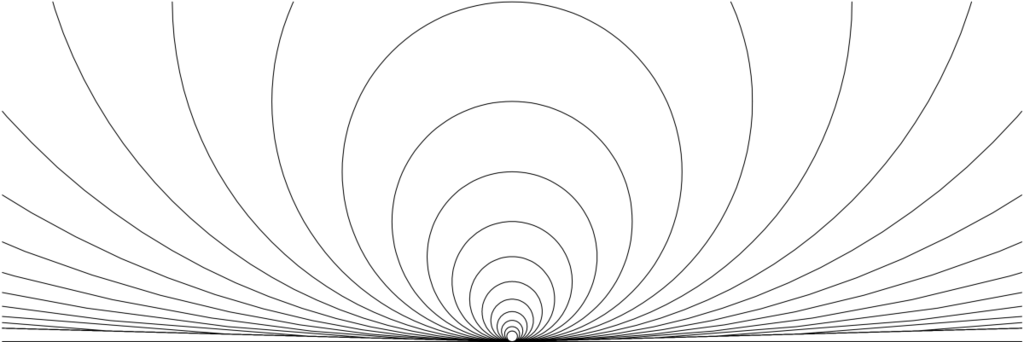
Stereographic projection satisfies surprising geometric conditions. First, circles on the sphere map to circles in the plane. This is plausible for circles in planes parallel to \(P\), but more remarkable for “tilted” circles. Second and conversely, every circle in the plane is the stereographic image of some circle on the sphere. There is a dictionary between circles on the sphere and circles in the plane.
In this dictionary, circles through the point \(p\) at infinity map to circles of infinite radius, i.e., to lines! To be explicit, we have introduced two distinct uses of “infinity”: A location on the sphere, and the “radius” of a line viewed as a circle. These two uses of “infinity” mesh geometrically when we speak of the “circle dictionary” under stereographic projection.
A third property of stereographic projection accounts for its place of high esteem at Differential Geometry: Stereographic projection is angle-preserving, or conformal. Particularly, if two curves, circles or otherwise, meet perpendicularly on the sphere, then their “stereographic shadows” meet perpendicularly in the plane.
Möbius Transformations
A conformal transformation of the sphere is called a Möbius Transformation. We can identify some of them from plane geometry. There are spatial rotations about the center of the sphere, which preserve angles in space, and more specifically preserve angles tangent to the sphere. (Reflections in planes through the center of the sphere preserve “absolute” angles, but exchange counterclockwise with clockwise, and in our sense therefore do not “preserve” angles.)

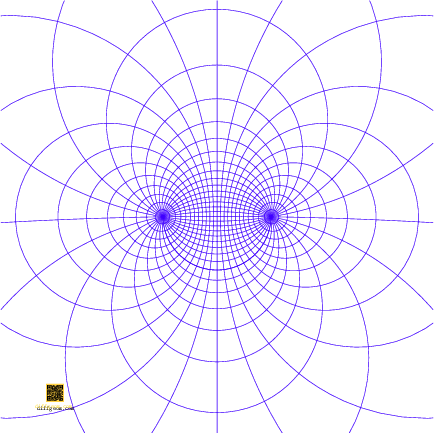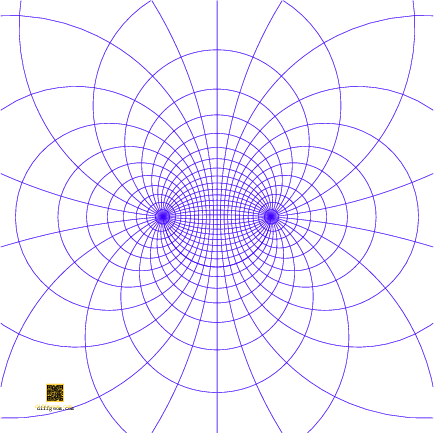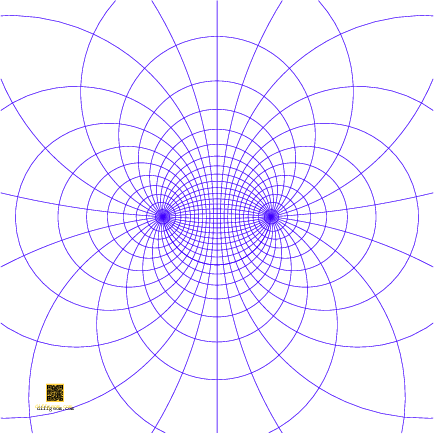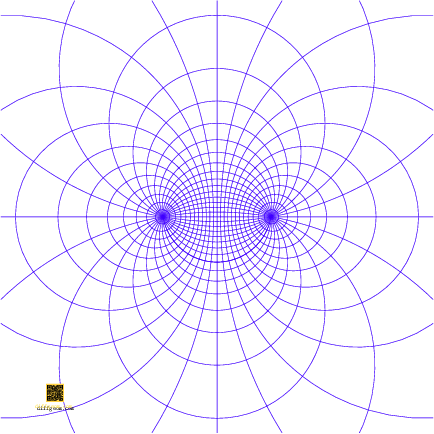
Other classes of conformal transformations are induced by rigid plane motions—translations and rotations—and scaling. It turns out that every Möbius transformation is a composition of rotations of the sphere, and translations and dilations of the plane:
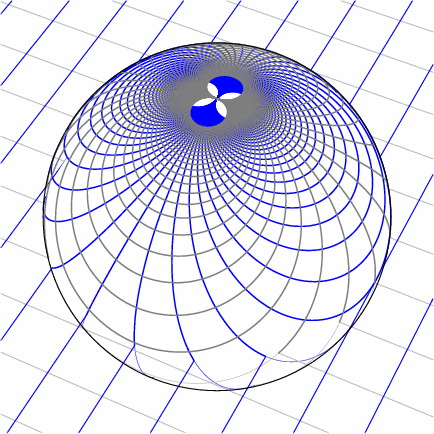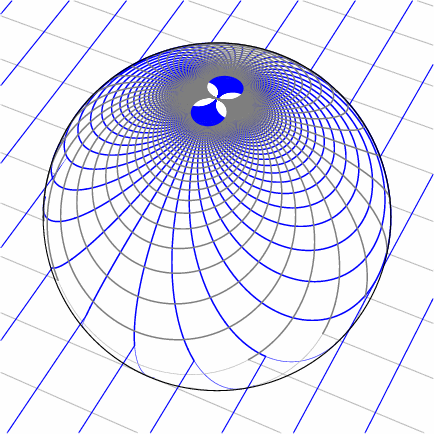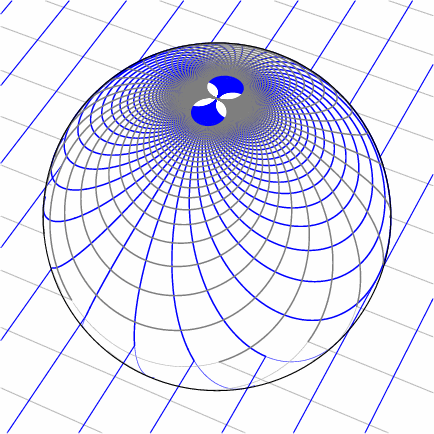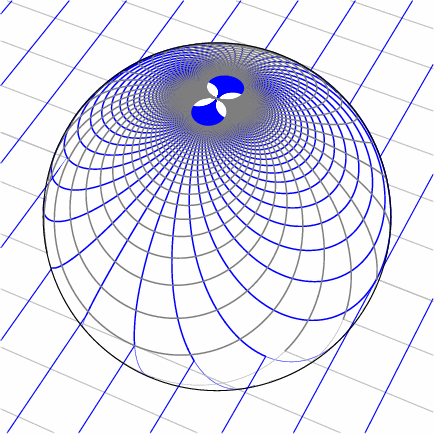
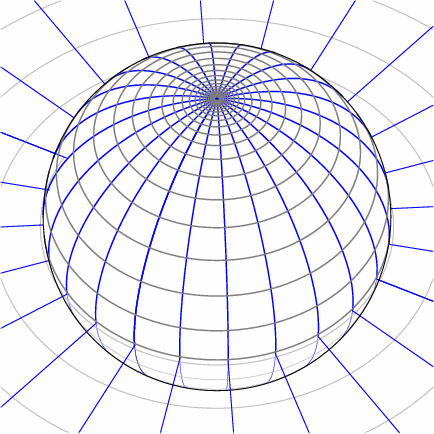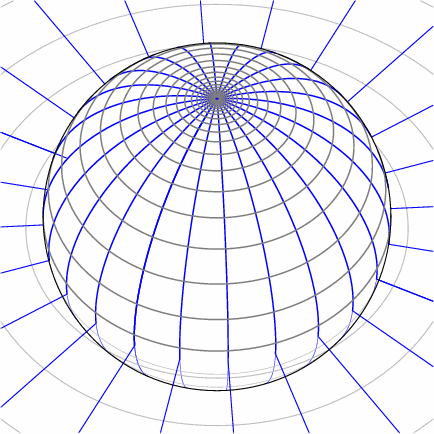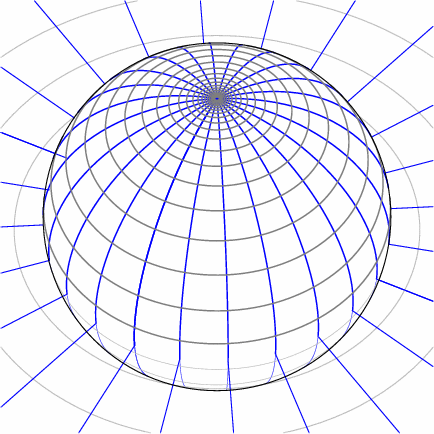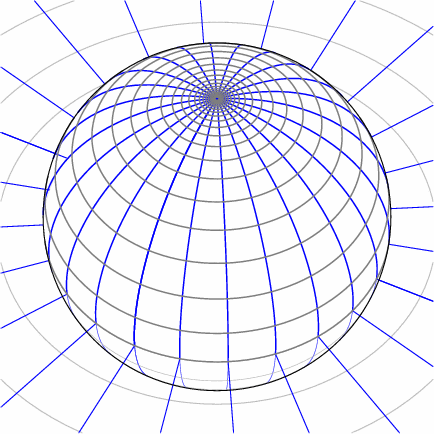
Möbius transformations have particularly beautiful geometry. An excellent introduction is the award-winning short film Möbius Transformations Revealed by Douglas Arnold and Jonathan Rogness at the University of Minnesota.
Here is an interactive web program for working with Möbius transformations on the sphere.
A number of images at Differential Geometry, including loxodromes, Möbius flow, and tendrils, depict the motions of point particles under “one parameter groups” of Möbius transformations.

If your appetite is whetted, introductory textbooks on complex analysis cover these topics in detail. Other search terms include “hyperbolic geometry” and “Lie sphere geometry”. (Sophus Lie, pronounced Lee, was a 19th century Norwegian mathematician, best-known among modern students for his foundational work on symmetry.)
Shadows from Higher Dimensions
Point projection, stereographic projection, and Möbius transformations extend to arbitrary dimensions. Rectangular coordinates give a convenient algebraic description, and are helpful for working with these geometric ideas in four-space. Our cyclide images at Differential Geometry arise by projecting a surface in four-space. If formulas are off-putting, you can safely skip the rest of this post, and instead explore by selecting the “cyclide” menu option in this interactive software.
If we choose rectangular coordinates \((x, y, z)\) so that the screen \(P\) has equation \(z = 0\), and we put \(p\) on the \(z\)-axis at \((0, 0, h)\) for some positive real number \(h\), then similar triangles can be used to show \[ \Pi(x, y, z) = \frac{h}{h – z}(x, y, 0). \] As consistency checks:
- This is undefined where \(z = h\), namely in the plane through \(p\) and parallel to \(P\).
- Where \(z = 0\), the multiplier on the right is \(h/(h – 0) = h/h = 1\), so \(\Pi(x, y, 0) = (x, y, 0)\). Geometrically, points of \(P\) project to themselves.
Point projection makes sense in higher-dimensional spaces. Let’s break down how this works step by step.
The formula for projection in four-space has one additional coordinate. Our “screen” is three-dimensional, with coordinates \((w, x, y, 0)\); our “light” is at \((0, 0, 0, h)\). The projection formula is \[ \Pi(w, x, y, z) = \frac{h}{h – z}(w, x, y, 0). \] We view the right-hand side as a point of three-space by discarding the final coordinate \(0\).
A straightforward way to define a torus in four-space is to pick constants \(a\) and \(b\) satisfying \(a^{2} + b^{2} = 1\), and consider the parametric formula \[ (w, x, y, z) = (a\cos u, a\sin u, b\cos v, b\sin v). \] Points of this form lie on the “ordered product” of a circle of radius \(a\) and a circle of radius \(b\). This surface is a “torus” lying in the sphere of unit radius in four-space. Plugging into our projection formula gives a particularly pleasant parametric description of a torus: \[ (u, v) \mapsto \frac{h}{h – b\sin v}(a\cos u, a\sin u, b\cos v). \]
We can, further, use rectangular coordinates to rotate our torus in four-space before casting its shadow in three-space! Rotating the \((w, z)\)-plane by an angle \(\theta\) is given by the formula \[ (w, x, y, z) \mapsto (w\cos\theta – z\sin\theta, x, y, z\cos\theta + w\sin\theta). \] Setting \(w = a\cos u\), \(x = a\sin u\), \(y = b\cos v\), and \(z = b\sin v\) gives the parametric surface \[ (u, v) \mapsto (a\cos u\cos\theta – b\sin v\sin\theta, a\sin u, b\cos v, b\sin v\cos\theta + a\cos u\sin\theta). \] Plugging this into the point projection formula gives \[ (u, v) \mapsto \frac{h}{h – (b\sin v\cos\theta + a\cos u\sin\theta)}(a\cos u\cos\theta – b\sin v\sin\theta, a\sin u, b\cos v). \] Plotting this parametric surface gives a “distorted” torus. When we rotate our torus in four-space, part of the surface moves closer to the light, and casts a larger shadow. If we rotate the torus until the light source lies on the torus, the projected surface in three-space, a parabolic cyclide, “passes through infinity” and cuts three-space into two linked solid pieces.
We’re free to debate whether or not four-space “exists.” In any case these formulas conform to our three-dimensional geometric expectations!