\(\newcommand{\R}{\mathbf{R}}\newcommand{\Vec}[1]{\boldsymbol{#1}}\newcommand{\e}{\Vec{e}}\renewcommand{\v}{\Vec{v}}\newcommand{\x}{\Vec{x}}\newcommand{\y}{\Vec{y}}\newcommand{\z}{\Vec{z}}\newcommand{\0}{\Vec{0}}\)[This blog post, taken from the students’ preface of my free (gratis) one-semester book Linear Algebra (2015), but also containing links to interactive software, gives a capsule summary of elementary linear algebra.]
Linear algebra comprises a variety of topics and viewpoints, including computational machinery (matrices), abstract objects (vector spaces), mappings (linear transformations), and the “fine structure” of linear transformations (diagonalizability).
Like all mathematical subjects at an introductory level, linear algebra is driven by examples and comprehended by unfamiliar theory. Each of the preceding topics can be difficult to assimilate until the others are understood. You, the reader, consequently face a chicken-and-egg problem: Examples appear unconnected without a theoretical framework, but theory without examples tends to be dry and unmotivated.
This preface sketches an overview of the entire book by looking at a family of representative examples. The “universe” is the ordered plane \(\R^{2}\), whose coordinates we denote \((x^{1}, x^{2})\). (The use of indices instead of the more familiar \((x, y)\) will economize our use of letters, particularly when we begin to study functions of arbitrarily many variables. The use of superscripts as indices rather than as exponents highlights important, subtle structure in formulas.) We view ordered pairs as individual entities, and write \(\x = (x^{1}, x^{2})\).
Vectors and Vector Spaces
We view an ordered pair \(\x\) as a vector, a type of object that can be added to another vector, or multiplied by a real constant (called a scalar) to obtain another vector. If \(\x = (x^{1}, x^{2})\) and \(\y = (y^{1}, y^{2})\), and if \(c\) is a scalar, we define \[ \x + \y = (x^{1} + y^{1}, x^{2} + y^{2}),\quad c\x = (cx^{1}, cx^{2}). \] The set \(\R^{2}\) equipped with these operations is said to be a vector space.
The vector \(\x = (x^{1}, x^{2})\) in the plane may be viewed geometrically as the arrow with its tail at the origin \(\0 = (0, 0)\) and its tip at the point \(\x\). Vector addition corresponds to forming the parallelogram with sides \(\x\) and \(\y\), and taking \(\x + \y\) to be the far corner. Scalar multiplication \(c\x\) corresponds to “stretching” \(\x\) by a factor of \(c\) if \(c > 0\), or to stretching by a factor of \(|c|\) and reversing the direction if \(c < 0\).
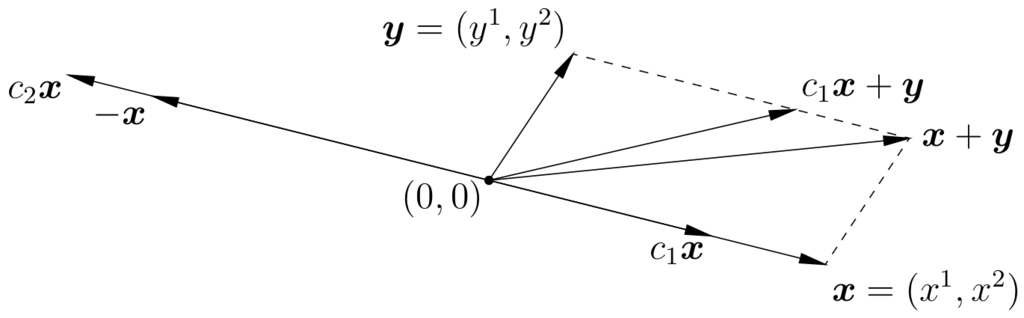
Linear Transformations
In linear algebra, most mappings send vector spaces to vector spaces. The special properties dictated by linear algebra may be written \[ \left. \begin{aligned} S(\x + \y) &= S(\x) + S(\y), \\ S(c\x) &= cS(\x) \end{aligned}\right\} \qquad\text{for all vectors \(\x\), \(\y\), all scalars \(c\).} \] For technical convenience, these conditions are often expressed as a single condition \[ S(c\x + \y) = cS(\x) + S(\y) \qquad\text{for all vectors \(\x\), \(\y\), all scalars \(c\).} \] A mapping \(S\) satisfying this conditions is called a linear transformation.
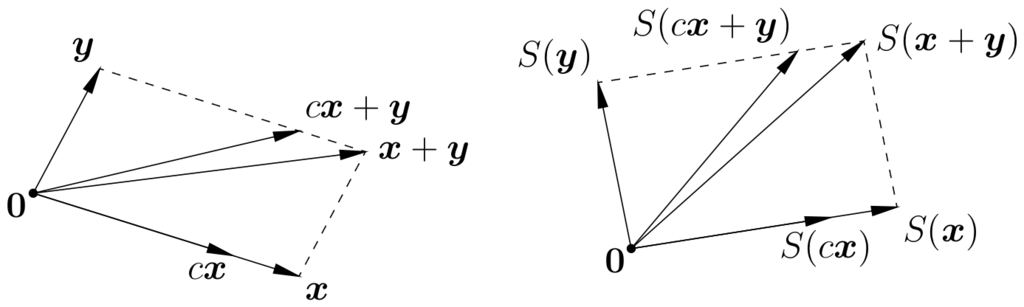
Geometrically, if \(\x\) and \(\y\) are arbitrary vectors and \(c\) is a scalar, so that \(c\x + \y\) is the far corner of the parallelogram with sides \(c\x\) and \(\y\), then \(S(c\x + \y) = cS(\x) + S(\y)\) is the far corner of the parallelogram with sides \(S(c\x) = cS(\x)\) and \(S(\y)\). A linear transformation \(S\) therefore maps an arbitrary parallelogram to a parallelogram in an obvious (and restrictive) sense.
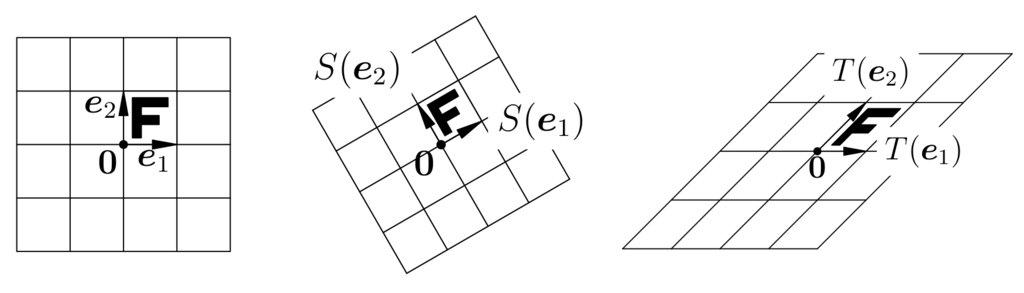
The special vectors \(\e_{1} = (1, 0)\) and \(\e_{2} = (0, 1)\) are the standard basis of \(\R^{2}\). Every vector in \(\R^{2}\) can be expressed uniquely as a linear combination: \begin{align*} \x = (x^{1}, x^{2}) &= (x^{1}, 0) + (0, x^{2}) \\ &= x^{1}(1, 0) + x^{2}(0, 1) \\ &= x^{1}\e_{1} + x^{2}\e_{2}. \end{align*} Formally, a linear transformation “distributes” over an arbitrary linear combination. In detail, if \(S:\R^{2} \to \R^{2}\) is a linear transformation, repeated application of the defining properties gives \begin{align*} S(\x) &= S(x^{1}\e_{1} + x^{2}\e_{2}) \\ &= S(x^{1}\e_{1}) + S(x^{2}\e_{2}) \\ &= x^{1}S(\e_{1}) + x^{2}S(\e_{2}). \end{align*} This innocuous equation expresses a remarkable conclusion: A linear transformation \(S:\R^{2} \to \R^{2}\) is completely determined by its values \(S(\e_{1})\), \(S(\e_{2})\) at two vectors.
Matrix Representation
To study vector spaces and linear transformations in greater detail, we will represent vectors and linear transformations as rectangular arrays of numbers, called matrices. The first chapter of the book introduces matrix notation, a central piece of computational machinery in linear algebra. Here we focus on motivation and geometric intuition, using the special case of linear transformations from the plane to the plane.
We use the notational convention in which vectors are written as columns: \[ \x = (x^{1}, x^{2}) = \left[\begin{array}{@{}c@{}} x^{1} \\ x^{2} \\ \end{array}\right]. \] With this notation, a linear transformation \(S:\R^{2} \to \R^{2}\) is completely and uniquely specified by scalars \(A_{i}^{j}\) satisfying \[ S(\e_{1}) = A_{1}^{1} \e_{1} + A_{1}^{2} \e_{2} = \left[\begin{array}{@{}c@{}} A_{1}^{1} \\ A_{1}^{2} \\ \end{array}\right],\quad S(\e_{2}) = A_{2}^{1} \e_{1} + A_{2}^{2} \e_{2} = \left[\begin{array}{@{}c@{}} A_{2}^{1} \\ A_{2}^{2} \\ \end{array}\right]. \] The (standard) matrix of \(S\) assembles these into a rectangular array \(A\): \[ A = \left[\begin{array}{@{}cc@{}} S(\e_{1}) & S(\e_{2}) \\ \end{array}\right] = \left[\begin{array}{@{}cc@{}} A_{1}^{1} & A_{2}^{1} \\ A_{1}^{2} & A_{2}^{2} \\ \end{array}\right]. \] The real number \(A_{j}^{i}\) in the \(i\)th row and \(j\)th column of \(A\) is called the \((i, j)\)-entry, and encodes the dependence of the \(i\)th output variable on the \(j\)th input variable.
Matrix Multiplication
For all \(\x\), we have \begin{align*} S(\x) &= x^{1}S(\e_{1}) + x^{2}S(\e_{2}) \\ &= x^{1} \left[\begin{array}{@{}c@{}} A_{1}^{1} \\ A_{1}^{2} \\ \end{array}\right] + x^{2} \left[\begin{array}{@{}c@{}} A_{2}^{1} \\ A_{2}^{2} \\ \end{array}\right] = \left[\begin{array}{@{}c@{}} A_{1}^{1} x^{1} + A_{2}^{1} x^{2} \\ A_{1}^{2} x^{1} + A_{2}^{2} x^{2} \\ \end{array}\right]. \end{align*} The expression on the right may be interpreted as a type of “product” of the matrix of \(S\) and the column vector of \(\x\): \[ \left[\begin{array}{@{}c@{}} y^{1} \\ y^{2} \\ \end{array}\right] = \left[\begin{array}{@{}c@{}} A_{1}^{1} x^{1} + A_{2}^{1} x^{2} \\ A_{1}^{2} x^{1} + A_{2}^{2} x^{2} \\ \end{array}\right] = \left[\begin{array}{@{}cc@{}} A_{1}^{1} & A_{2}^{1} \\ A_{1}^{2} & A_{2}^{2} \\ \end{array}\right] \left[\begin{array}{@{}c@{}} x^{1} \\ x^{2} \\ \end{array}\right], \] or simply \(\y = A\x\). The second equality defines the product of the “\(2 \times 2\) square matrix \(A\)” and the “\(2 \times 1\) column matrix \(\x\)”.
Particularly when the number of variables is large, sigma (summation) notation comes into its own, both condensing common expressions and highlighting their structure. The relationship between the inputs \(x^{j}\) and the outputs \(y^{i}\) of a linear transformation may be written \(y^{i} = \sum_{j} A_{j}^{i} x^{j}\). (Physicists sometimes go further, omitting the summation sign and implicitly summing over every index that appears both as a subscript and as a superscript: \(y^{i} = A_{j}^{i} x^{j}\). This book does not use this “Einstein summation convention”, but the possibility of doing so explains our use of superscripts as indices, despite the potential risk of reading superscripts as exponents. Exponents appear so rarely in linear algebra that mentioning them at each occurrence is feasible.)
Composition of Linear Transformations
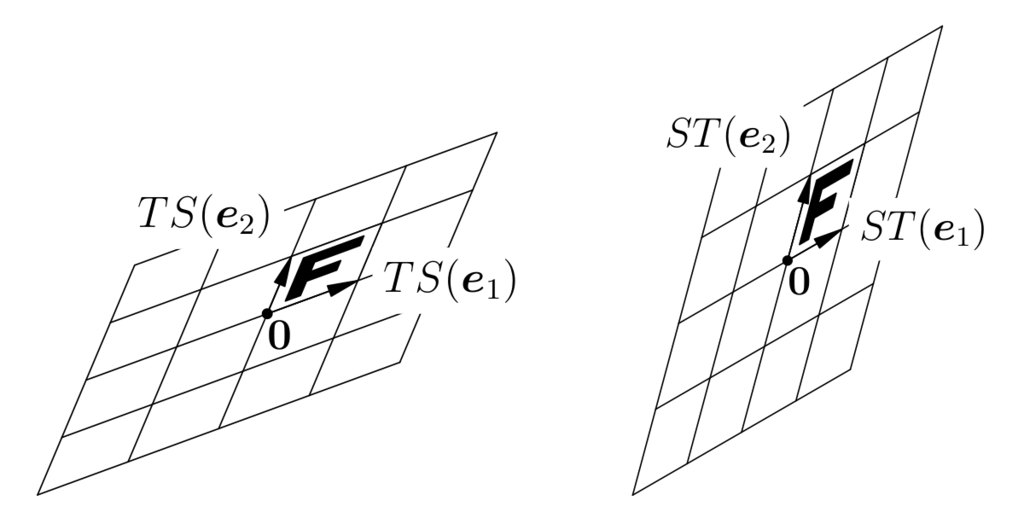
If \(T:\R^{2} \to \R^{2}\) is a linear transformation with matrix \[ B = \left[\begin{array}{@{}cc@{}} B_{1}^{1} & B_{2}^{1} \\ B_{1}^{2} & B_{2}^{2} \\ \end{array}\right], \] the composition \(T \circ S:\R^{2} \to \R^{2}\), defined by \((T \circ S)(\x) = T\bigl(S(\x)\bigr)\), is easily shown to be a linear transformation (check this). The associated matrix is a “product” of the matrices \(B\) and \(A\) of the transformations \(T\) and \(S\). To determine the entries of this product, note that by definition, \begin{align*} T(\e_{1}) &= B_{1}^{1} \e_{1} + B_{1}^{2} \e_{2}, & S(\e_{1}) &= A_{1}^{1} \e_{1} + A_{1}^{2} \e_{2}, \\ T(\e_{2}) &= B_{2}^{1} \e_{1} + B_{2}^{2} \e_{2}, & S(\e_{2}) &= A_{2}^{1} \e_{1} + A_{2}^{2} \e_{2}. \\ \end{align*} Consequently, \begin{align*} TS(\e_{1}) &= T(A_{1}^{1} \e_{1} + A_{1}^{2} \e_{2}) \\ &= A_{1}^{1} T(\e_{1}) + A_{1}^{2} T(\e_{2}) \\ &= A_{1}^{1}(B_{1}^{1} \e_{1} + B_{1}^{2} \e_{2}) + A_{1}^{2}(B_{2}^{1} \e_{1} + B_{2}^{2} \e_{2}) \\ &= (B_{1}^{1} A_{1}^{1} + B_{2}^{1} A_{1}^{2}) \e_{1} + (B_{1}^{2} A_{1}^{1} + B_{2}^{2} A_{1}^{2}) \e_{2}; \end{align*} similarly (check this), \begin{align*} TS(\e_{2}) &= (B_{1}^{1} A_{2}^{1} + B_{2}^{1} A_{2}^{2}) \e_{1} + (B_{1}^{2} A_{2}^{1} + B_{2}^{2} A_{2}^{2}) \e_{2}. \end{align*} Since the coefficients of \(T(\e_{1})\) give the first column of the matrix of \(TS\) and the coefficients of \(T(\e_{2})\) give the second column of the matrix, we are led to define the matrix product by \[ BA = \left[\begin{array}{@{}cc@{}} B_{1}^{1} & B_{2}^{1} \\ B_{1}^{2} & B_{2}^{2} \\ \end{array}\right] \left[\begin{array}{@{}cc@{}} A_{1}^{1} & A_{2}^{1} \\ A_{1}^{2} & A_{2}^{2} \\ \end{array}\right] = \left[\begin{array}{@{}cc@{}} B_{1}^{1} A_{1}^{1} + B_{2}^{1} A_{1}^{2} & B_{1}^{1} A_{2}^{1} + B_{2}^{1} A_{2}^{2} \\ B_{1}^{2} A_{1}^{1} + B_{2}^{2} A_{1}^{2} & B_{1}^{2} A_{2}^{1} + B_{2}^{2} A_{2}^{2} \\ \end{array}\right]. \] This forbidding collection of formulas is clarified by summation notation: \[ (BA)_{j}^{i} = \sum\nolimits_{k} B_{k}^{i} A_{j}^{k}. \] The preceding equation has precisely the same form for matrices of arbitrary size, and furnishes our general definition of matrix multiplication. (Convince yourself that the entries of \(BA\) are given by the preceding summation formula.)
When working computationally with specific matrices, the formula is generally less important than the procedure encoded by the formula. First, define the “product” of a “row” and a “column” by \[ \left[\begin{array}{@{}cc@{}} b & b’ \\ \end{array}\right]\left[\begin{array}{@{}l@{}} a \\ a’ \\ \end{array}\right] = \left[\begin{array}{@{}c@{}} ba + b’a’ \\ \end{array}\right]. \] Now, to find the \((i, j)\)-entry of the product \(BA\), multiply the \(i\)th row of \(B\) by the \(j\)th column of \(A\). For example, to find the entry in the first row and second column of \(BA\), multiply the first row of \(B\) by the second column of \(A\).
Geometry of Linear Transformations
Consider the linear transformation \(S\) that rotates \(\R^{2}\) about the origin by \(\frac{\pi}{6}\), and \(T\) that shears the plane horizontally by one unit:
The matrix of each may be read off the images of the standard basis vectors. Thus, \begin{align*} A &= \left[\begin{array}{@{}cc@{}} S(\e_{1}) & S(\e_{2}) \\ \end{array}\right] = \left[\begin{array}{@{}cc@{}} \cos \tfrac{\pi}{6} & \cos \tfrac{2\pi}{3} \\ \sin \tfrac{\pi}{6} & \sin \tfrac{2\pi}{3} \\ \end{array}\right] = \tfrac{1}{2} \left[\begin{array}{@{}cc@{}} \sqrt{3} & -1 \\ 1 & \sqrt{3} \end{array}\right], \\ B &= \left[\begin{array}{@{}cc@{}} T(\e_{1}) & T(\e_{2}) \\ \end{array}\right] = \left[\begin{array}{@{}cc@{}} 1 & 1 \\ 0 & 1 \\ \end{array}\right]. \end{align*}
The composite transformations \(TS\) (rotate, then shear) and \(ST\) (shear, then rotate) are linear, and their matrices may be found by matrix multiplication: \[ BA = \tfrac{1}{2} \left[\begin{array}{@{}cc@{}} \sqrt{3} + 1 & \sqrt{3} – 1 \\ 1 & \sqrt{3} \\ \end{array}\right],\qquad AB = \tfrac{1}{2} \left[\begin{array}{@{}cc@{}} \sqrt{3} & \sqrt{3} – 1 \\ 1 & \sqrt{3} + 1 \\ \end{array}\right]. \] Note carefully that \(TS \neq ST\). Composition of linear transformations, and consequently multiplication of square matrices, is generally a non-commutative operation.
Diagonalization
The so-called identity matrix \[ \left[\begin{array}{@{}cc@{}} 1 & 0 \\ 0 & 1 \\ \end{array}\right] \] corresponds to the identity mapping \(I(\x) = \x\) for all \(\x\) in \(\R^{2}\). Generally, if \(\lambda^{1}\) and \(\lambda^{2}\) are real numbers, the diagonal matrix \[ \left[\begin{array}{@{}cc@{}} \lambda^{1} & 0 \\ 0 & \lambda^{2} \\ \end{array}\right] \] corresponds to axial scaling, \((x^{1}, x^{2}) \mapsto (\lambda^{1}x^{1}, \lambda^{2}x^{2})\). Diagonal matrices are among the simplest matrices. In particular, if \(n\) is a positive integer, the \(n\)th power of a diagonal matrix is trivially calculated: \[ \left[\begin{array}{@{}cc@{}} \lambda^{1} & 0 \\ 0 & \lambda^{2} \\ \end{array}\right]^{n} = \left[\begin{array}{@{}cc@{}} (\lambda^{1})^{n} & 0 \\ 0 & (\lambda^{2})^{n} \\ \end{array}\right]. \]
The solution to a variety of mathematical problems rests on our ability to compute arbitrary powers of a matrix. We are naturally led to ask: If \(S:\R^{2} \to \R^{2}\) is a linear transformation, does there exist a coordinate system in which \(S\) acts by axial scaling? This question turns out to reduce to existence of scalars \(\lambda^{1}\) and \(\lambda^{2}\), and of non-zero vectors \(\v_{1}\) and \(\v_{2}\), such that \[ S(\v_{1}) = \lambda^{1} \v_{1},\qquad S(\v_{2}) = \lambda^{2} \v_{2}. \] Each \(\lambda^{i}\) is an eigenvalue of \(S\); each \(\v_{i}\) is an eigenvector of \(S\). A pair of non-proportional eigenvectors in the plane is an eigenbasis for \(S\).
A linear transformation may or may not admit an eigenbasis. The rotation \(S\) of the preceding example has no real eigenvalues at all. The shear \(T\) has one real eigenvalue, and admits an eigenvector, but has no eigenbasis. The compositions \(TS\) and \(ST\) both turn out to admit eigenbases.
Structural Summary
Basic linear algebra has three parallel “levels”. In increasing order of abstraction, they are:
- (i) “The level of entries”: Column vectors and matrices written out as arrays of numbers. (\(y^{i} = \sum_{j} A_{j}^{i} x^{j}\).)
- (ii) “The level of matrices”: Column vectors and matrices written as single entities. (\(\y = A\x\).)
- (iii) “The abstract level”: Vectors (defined axiomatically) and linear transformations (mappings that distribute over linear combinations). (\(\y = S(\x)\).)
Linear algebra is, at heart, the study of linear combinations and mappings that “respect” them. Along your journey through the material, strive to detect the levels’ respective viewpoints and idioms. Among the most universal idioms is this: A linear combination of linear combinations is a linear combination.
Matrices are designed expressly to handle the bookkeeping details. In summation notation at level (i), if \[ z^{i} = \sum_{k=1}^{m} B_{k}^{i} y^{k}\quad\text{and}\quad y^{k} = \sum_{j=1}^{n} A_{j}^{k} x^{j}, \] then substitution of the second into the first gives \[ z^{i} = \sum_{k=1}^{m} B_{k}^{i} \sum_{j=1}^{n} A_{j}^{k} x^{j} = \sum_{j=1}^{n} \left(\sum_{k=1}^{m} B_{k}^{i} A_{j}^{k}\right) x^{j} = \sum_{j=1}^{n} (BA)_{j}^{i} x^{j}. \] Once we establish properties of matrix operations, the preceding can be distilled down to an extremely simple computation at level (ii): If \(\z = B\y\) and \(\y = A\x\), then \(\z = B(A\x) = (BA)\x\).
Organization of the Book
The first chapter introduces real matrices as formally and quickly as feasible. The goal is to construct machinery for flexible computation. The book proceeds to introduce vector spaces and their properties, two auxiliary pieces of algebraic machinery (the dot product, and the determinant function on square matrices, each of which has a useful geometric interpretation), linear transformations and their properties, and diagonalization.
Of necessity, the motivation for a particular definition may not be immediately apparent. At each stage, we are merely generalizing and systematizing the preceding summary. It may help to review this preface periodically as you proceed through the material.