Cantor's Staircase Hahnemühle German Etching Print

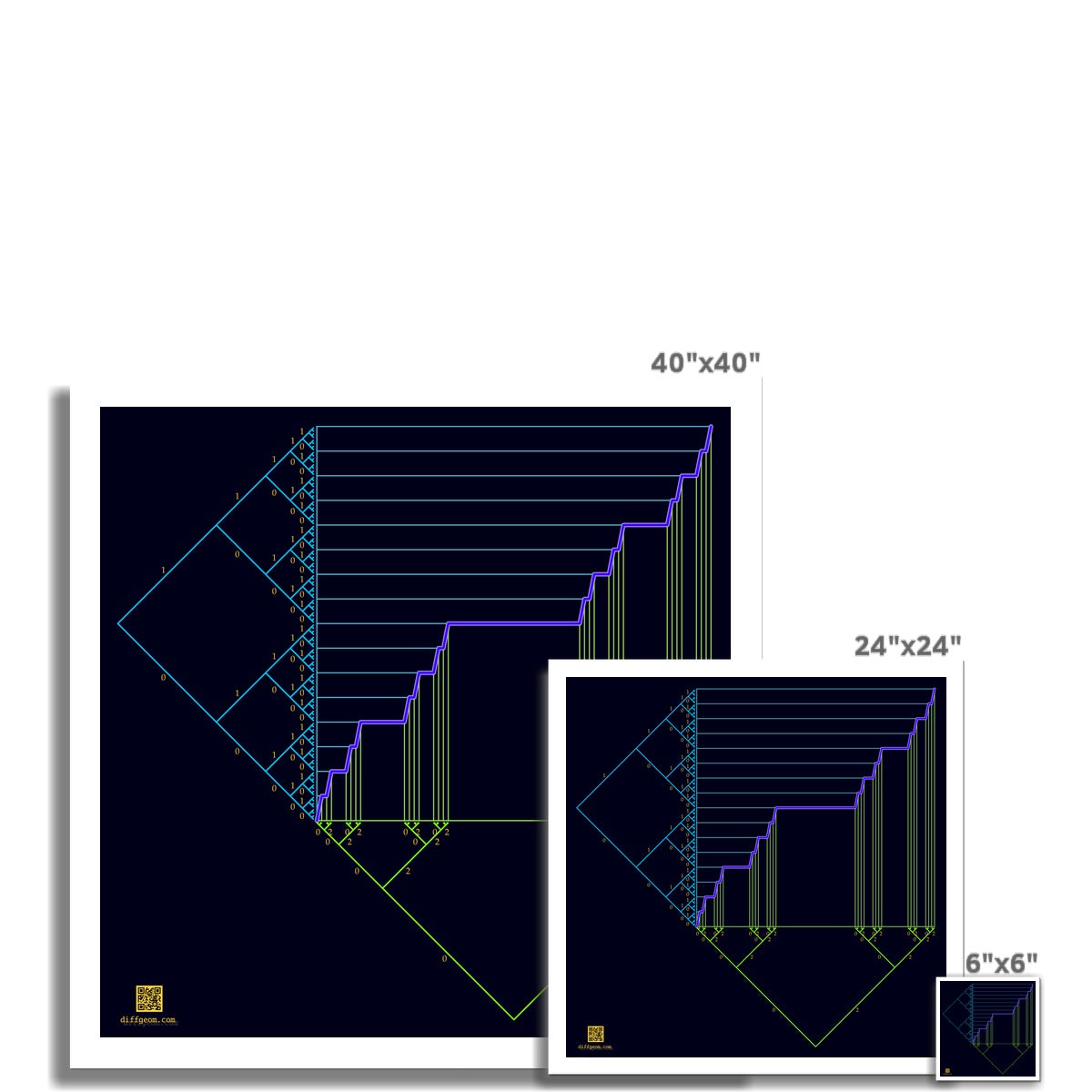
The Cantor ternary set is obtained from the closed unit interval by recursively removing open middle thirds of intervals. Points of the Cantor set correspond to limits of infinite ascending paths in the base-3 tree at bottom. Algebraically, these are base-3 "decimals" containing only the digits 0 and 2.

The closed unit interval may be viewed geometrically as the set of limits of infinite rightward paths in the base-2 tree at left. Algebraically, the closed unit interval is the set of binary "decimals," sequences of 0s and 1s to the right of a decimal point viewed as base-2.

The image shows a continuous mapping from the Cantor set onto the closed unit interval. Geometrically, each ascending path in the bottom tree gives rise to a unique rightward path in the left tree. Algebraically, take an infinite base-3 decimal with only 0s and 2s, divide each digit by 2, and interpret the result in base-2. The purple graph shows the extension that is continuous, and constant on the "middle thirds" intervals that are removed to form the Cantor set.

Printed on archival quality Hahnemühle German etching paper (310gsm) with a velvety surface.