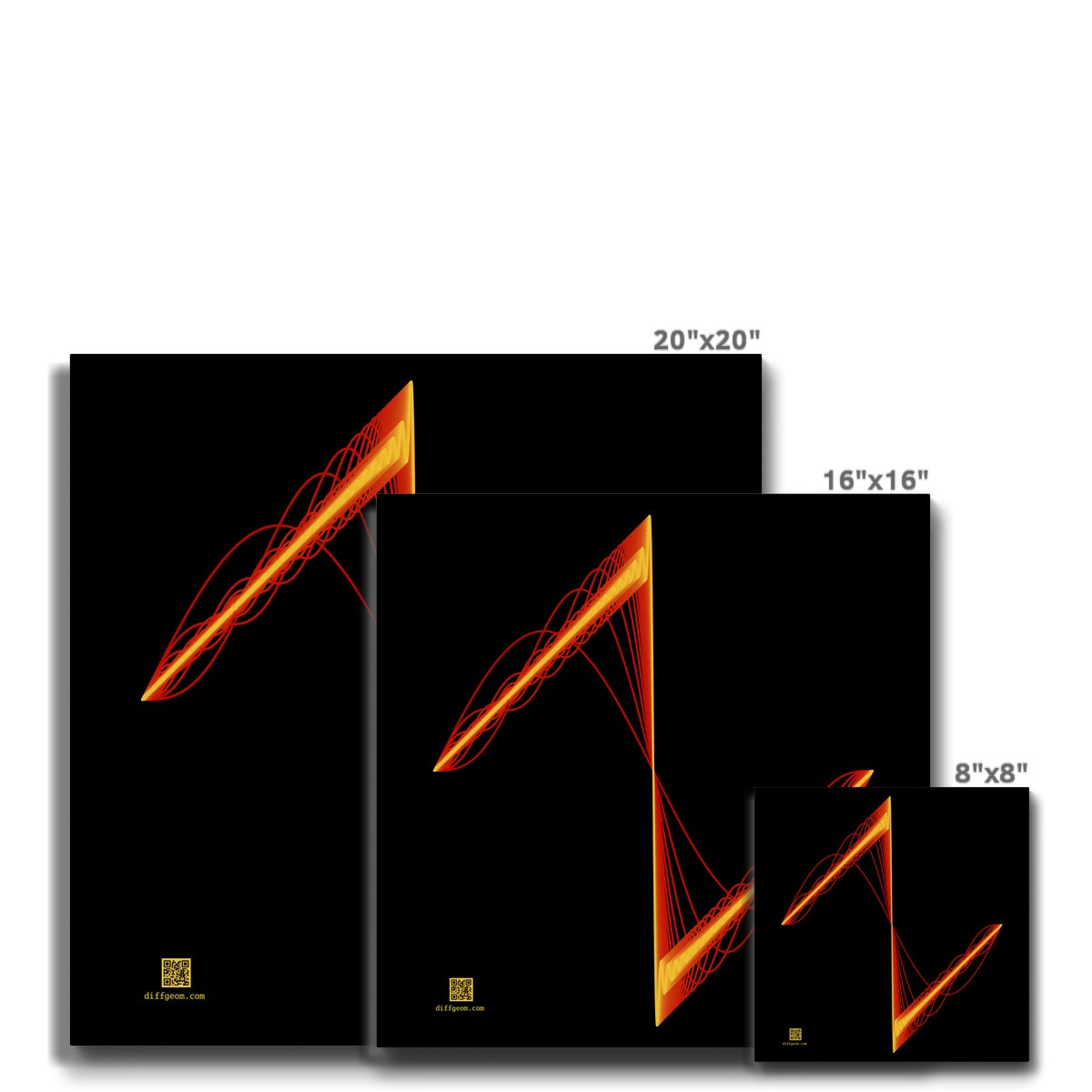
A "waveform" of wavelength L amounts to a function defined on the real interval [0, L], then extended so the graph repeats forever in both directions under shifting by whole multiples of L. A "piecewise-smooth" waveform can be written as a sum, over the positive integers n, of sines and cosines of period L/n (and an added constant). Musically, the trig functions are "pure tones" or "harmonics" and the "Fourier coefficients" in the sum are the "power spectrum" specifying how loud each harmonic is in the waveform. Adding up the first ten harmonics, say, gives an approximation known as the "tenth Fourier polynomial." When the signal is discontinuous, the sequence of Fourier polynomials exhibits "Gibbs' phenomenon": Spikes a bit more than 0.08 of the jump size form, and "compress" toward the discontinuity as the number of harmonics grows without bound. The image depicts this for 60 terms of a sawtooth approximation.
Made in the UK from recycled plastic bottles, stretched over a lightweight recycled frame. Packaging is also made from 100% recycled content.
