Line With Two Origins Fine Art Print

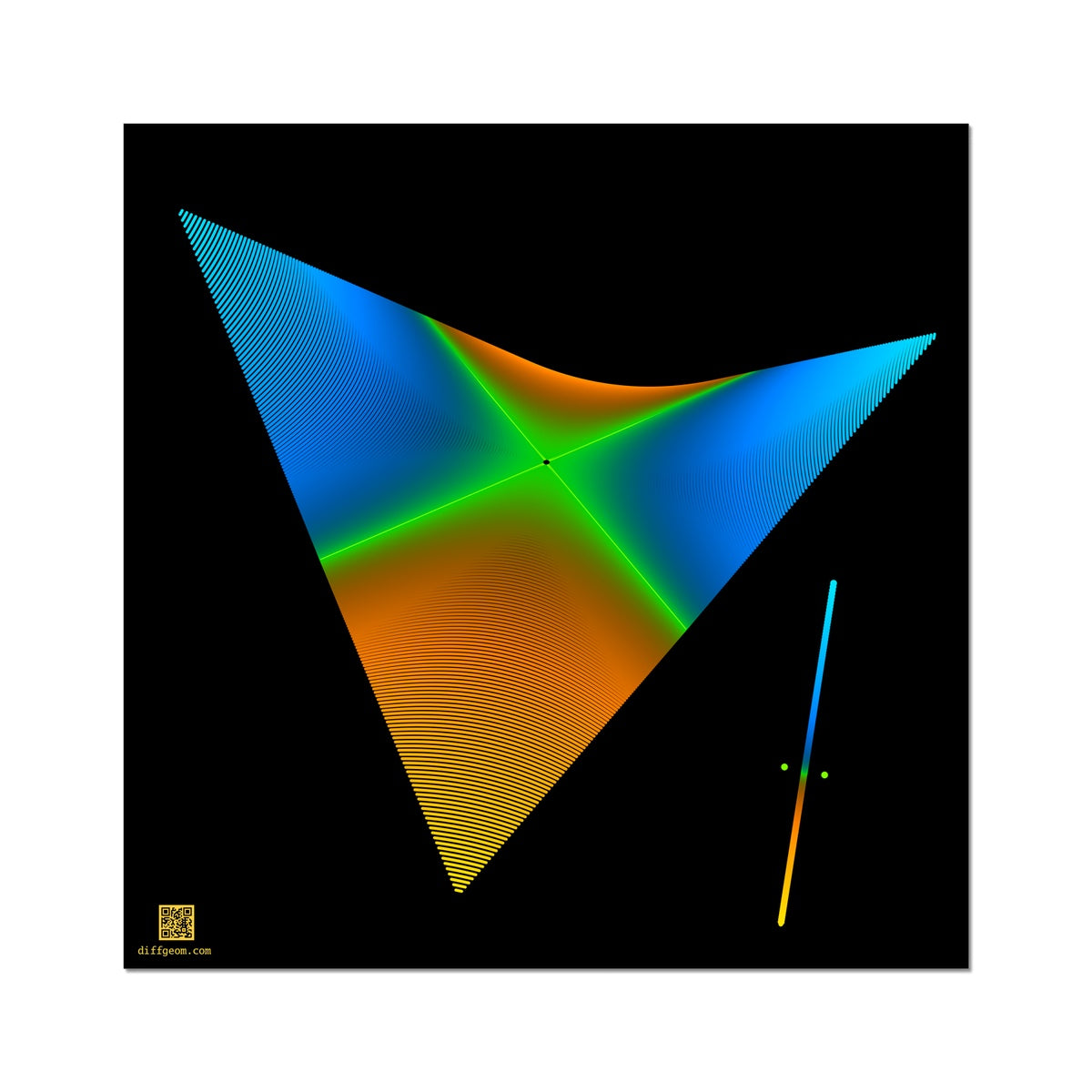
The line with two origins refers to the topological space obtained from two number lines by "gluing" each point of one line—except for the origin—to the corresponding point in the other line. Each point of the line with two origins has a neighborhood that looks just like an ordinary open interval, but the two origins, although distinct as points, cannot be separated by neighborhoods.

The line with two origins has a natural description in linear algebra as a quotient space of the plane with the origin removed. The additive group of reals cross the two-element group of signs, or \((\mathbf{R}, +) \times (\{\pm1\}, \cdot)\) acts by \(\gamma_{t, \pm}(x, y) = \pm(e^{t}x, e^{-t}y)\). For each non-zero height \(c\), the hyperbola \(xy = c\) is an orbit. The \(x\)-axis with the origin removed and \(y\)-axis with the origin removed are also orbits. The orbits are points of the quotient space. Each neighborhood of one axis is a deleted neighborhood of the other axis.

Printed on museum-quality fine art print paper (200 gsm) with a textured, matte finish.