Prodigi
Lorenz Attractor, Warm Fine Art Print
Lorenz Attractor, Warm Fine Art Print
Couldn't load pickup availability
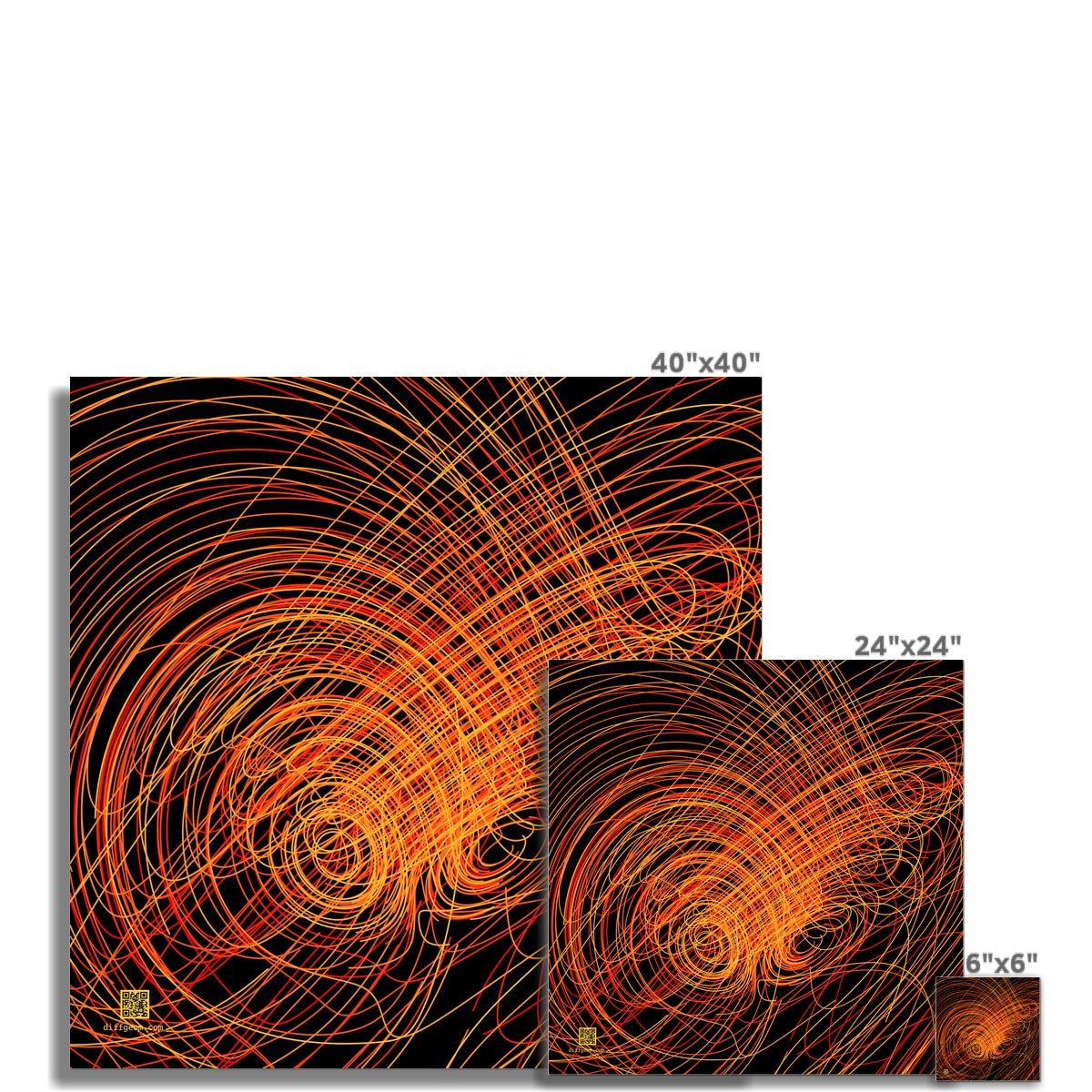
Simple equations have simple solutions. The assertion sounds reasonable, but over the 20th century mathematicians discovered how profoundly complicated dynamical systems can be merely by involving quadratic terms. Let \((x, y, z)\) denote spatial position, and let \(t\) represent time. In the 1960s, meteorologist Edward Lorenz and computer scientists Ellen Fetter and Margaret Hamilton studied a particularly simple-looking system of differential equations as a model of atmospheric convection: \begin{align*} \frac{dx}{dt} &= -10x + 10y, \\ \frac{dy}{dt} &= 28x - y - xz, \\ \frac{dz}{dt} &= xy - \tfrac{8}{3}z. \end{align*} An individual solution, rather than settling down to a point or loop as one might expect, instead moved unpredictably. Further, the qualitative behavior of solutions changed chaotically when the initial conditions were slightly varied. The image depicts randomly-chosen numerical solutions to the system. The two-lobed "strange attractor" that solutions "tend toward" can be glimpsed in the two eye-like loops near the center.
Printed on museum-quality fine art print paper (200 gsm) with a textured, matte finish.Share