Lotus, Moonlight Hahnemühle German Etching Print

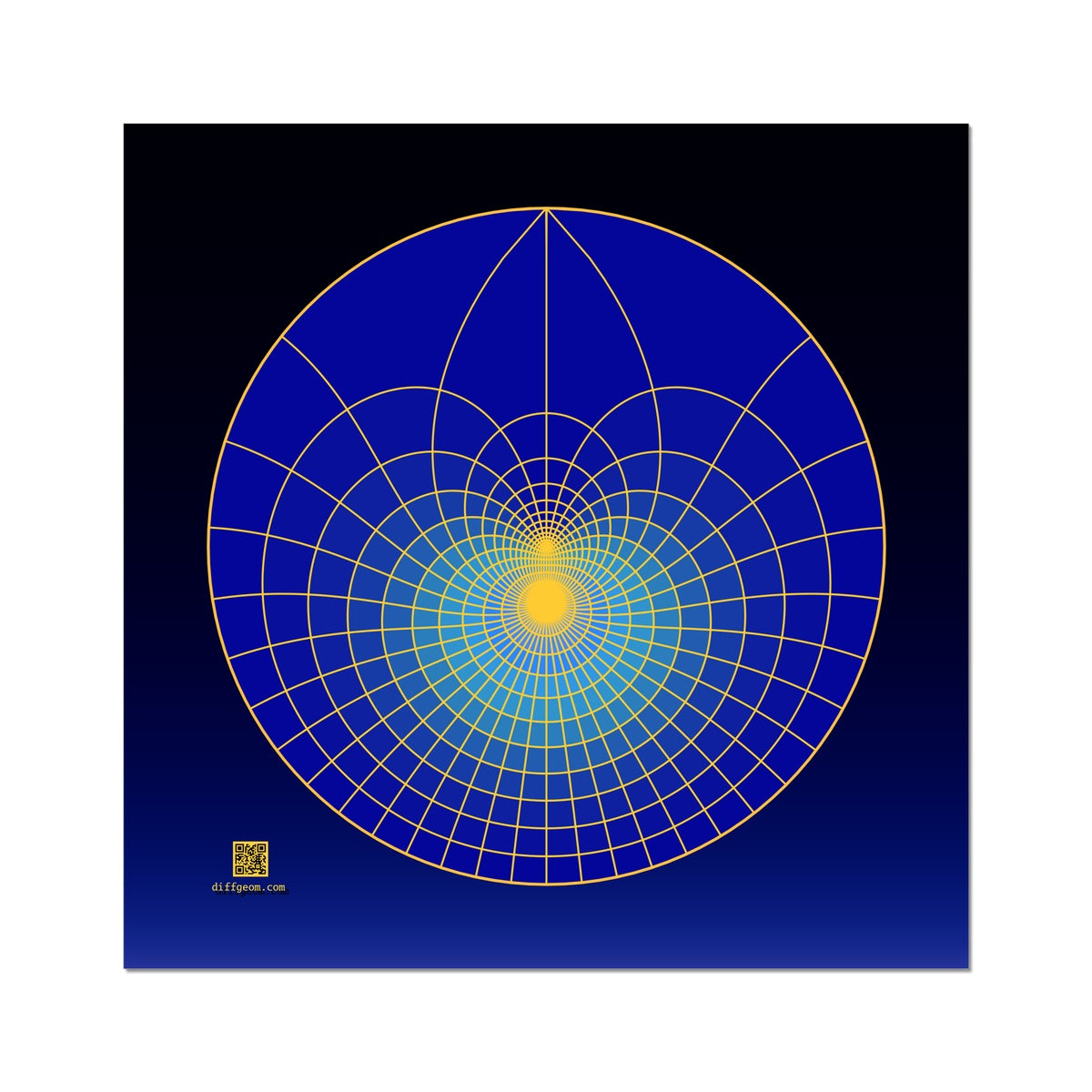
A non-empty open set in the plane is "simply-connected" if any two points of the set are joined by a path lying in the set, and if every closed path in the set can be "shrunk to a point" staying within the set. Qualitatively, the set is in one piece, and does not enclose any holes.

A disk, a rectangle, and the plane with a closed ray removed are simply-connected. A union of two disjoint disks, an annulus, and the plane with one or more points removed are not simply-connected.

A "conformal equivalence" of open sets is an invertible, complex-differentiable mapping. The Riemann mapping theorem asserts that any two simply-connected sets other than the plane itself are conformally equivalent. The lotus is the image of a polar coordinate grid under a conformal equivalence from the disk to the disk with the vertical radial ray removed.

Printed on archival quality Hahnemühle German etching paper (310gsm) with a velvety surface.