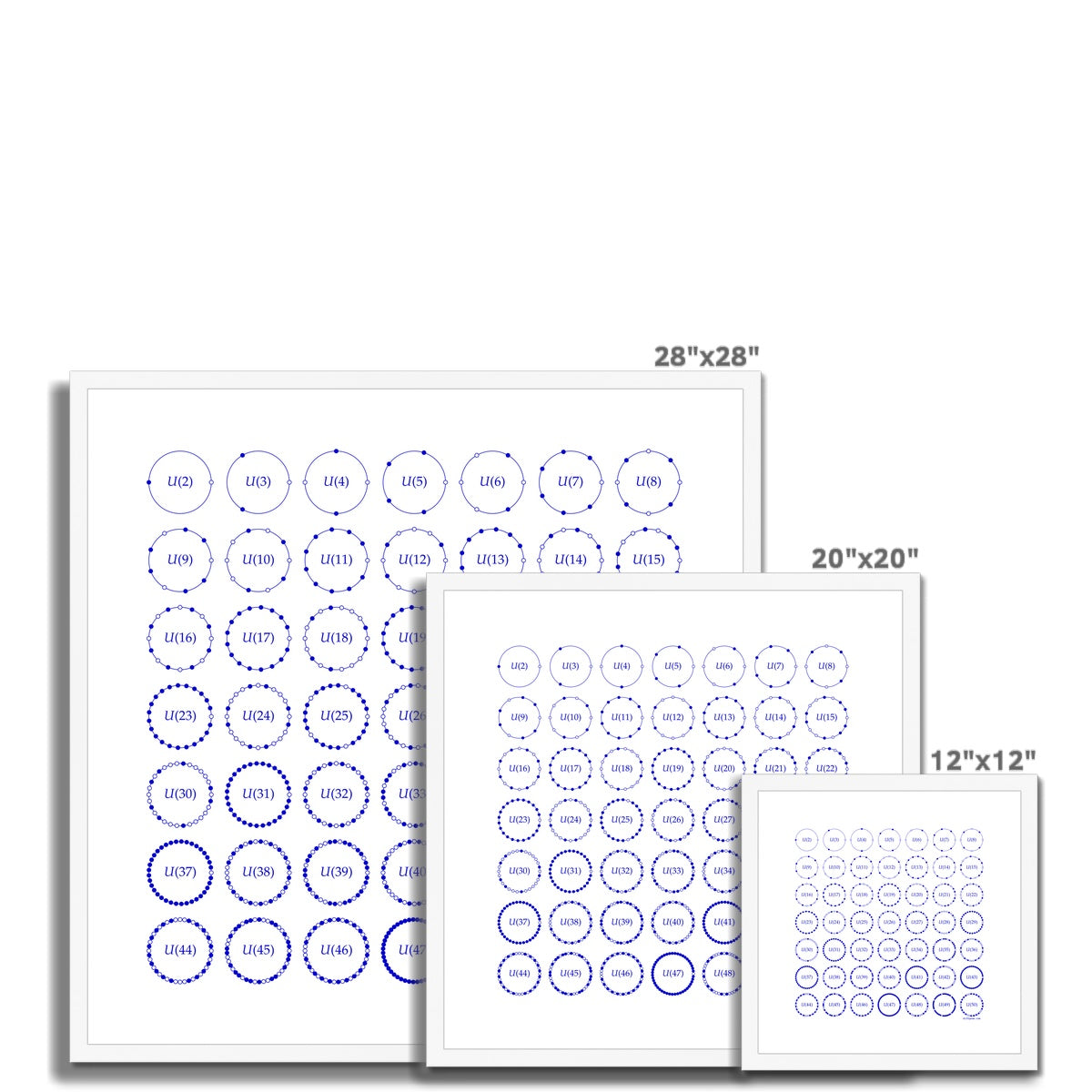
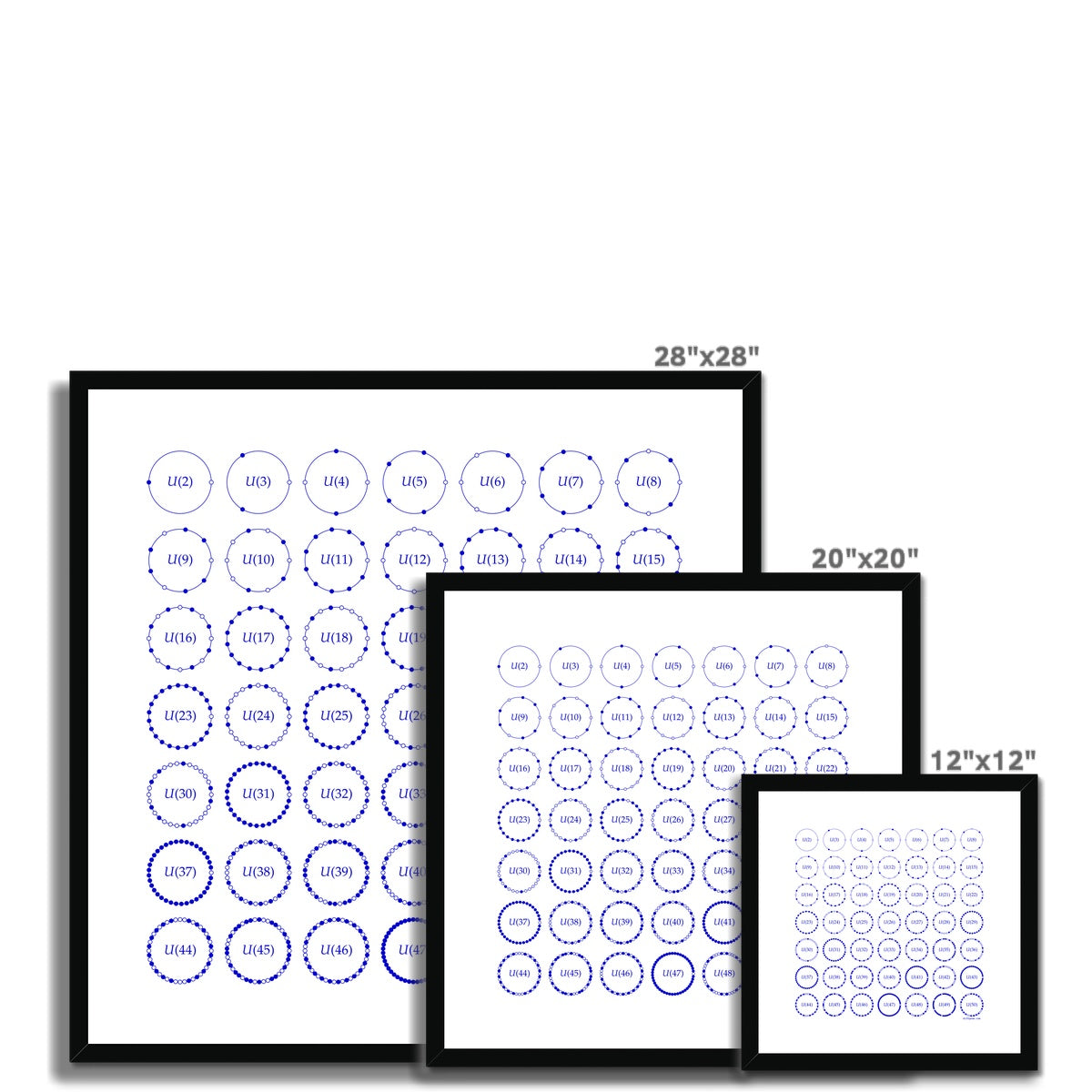
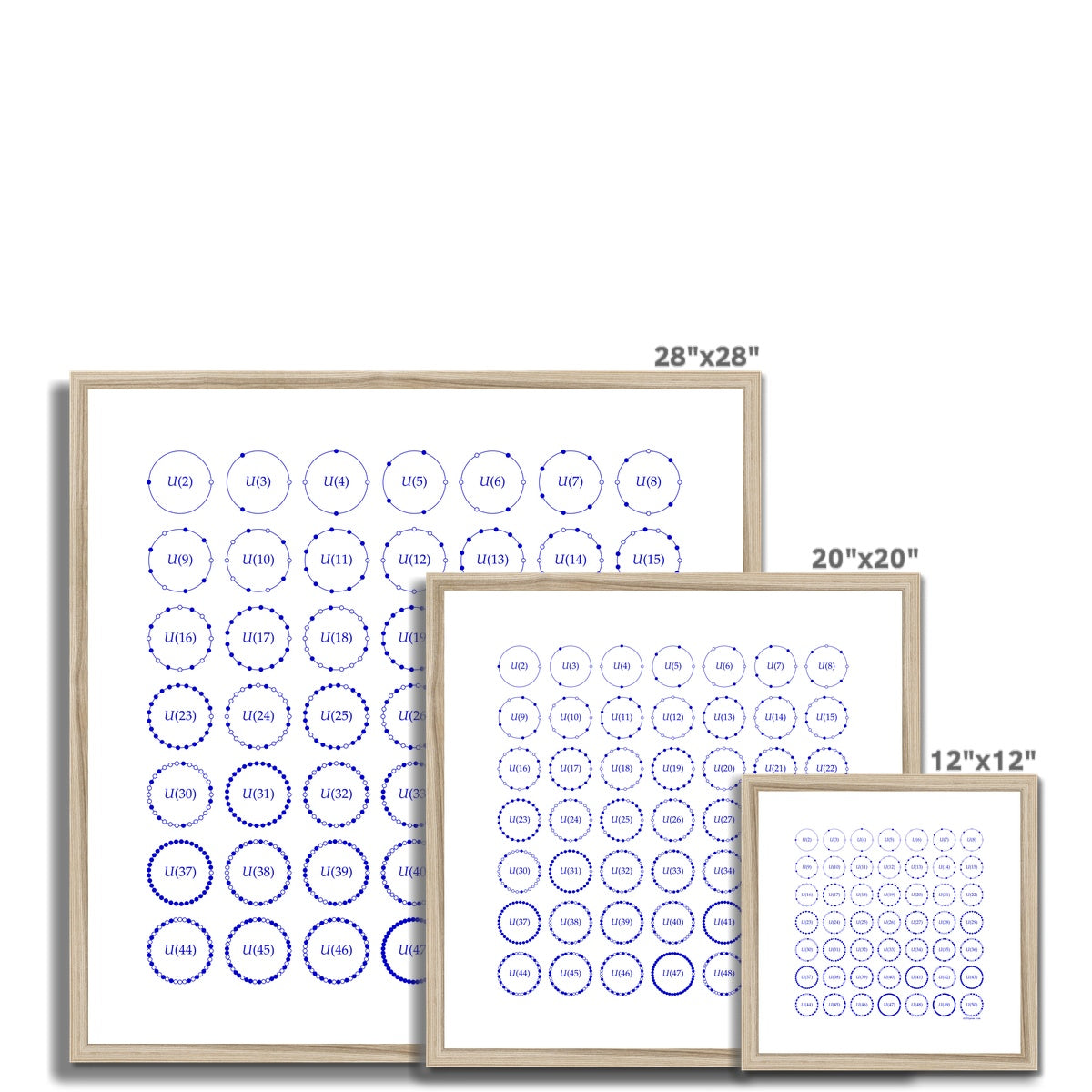
In the unit circle, inscribe a regular polygon with one vertex at the rightmost point, the complex number 1. The set of all vertices may be viewed as a finite "set of numbers." If the polygon has 25 sides, for example, mathematicians view the vertices as residue classes mod 25 and say the set of vertices implements arithmetic mod 25.
Take an arbitrary residue class and compute its set of integer powers. One of two alternatives must occur: Every residue class appears among the set of powers ("units"), or some residue classes do not appear as powers ("non-units"). For each modulus, the two alternatives are represented by filled dots (units) and unfilled dots.
The classification of residue classes into units and non-units is related to the prime factorization of the modulus. Particularly, the modulus is prime if and only if every residue class other than 1 is a unit.
Handmade in the UK by specialist picture framers using premium fine art paper with a gently textured surface and satin finish, high-quality wood, and an FSC certified off-white mat. Delivered ready for hanging.
