NaN
/
of
-Infinity
Prodigi
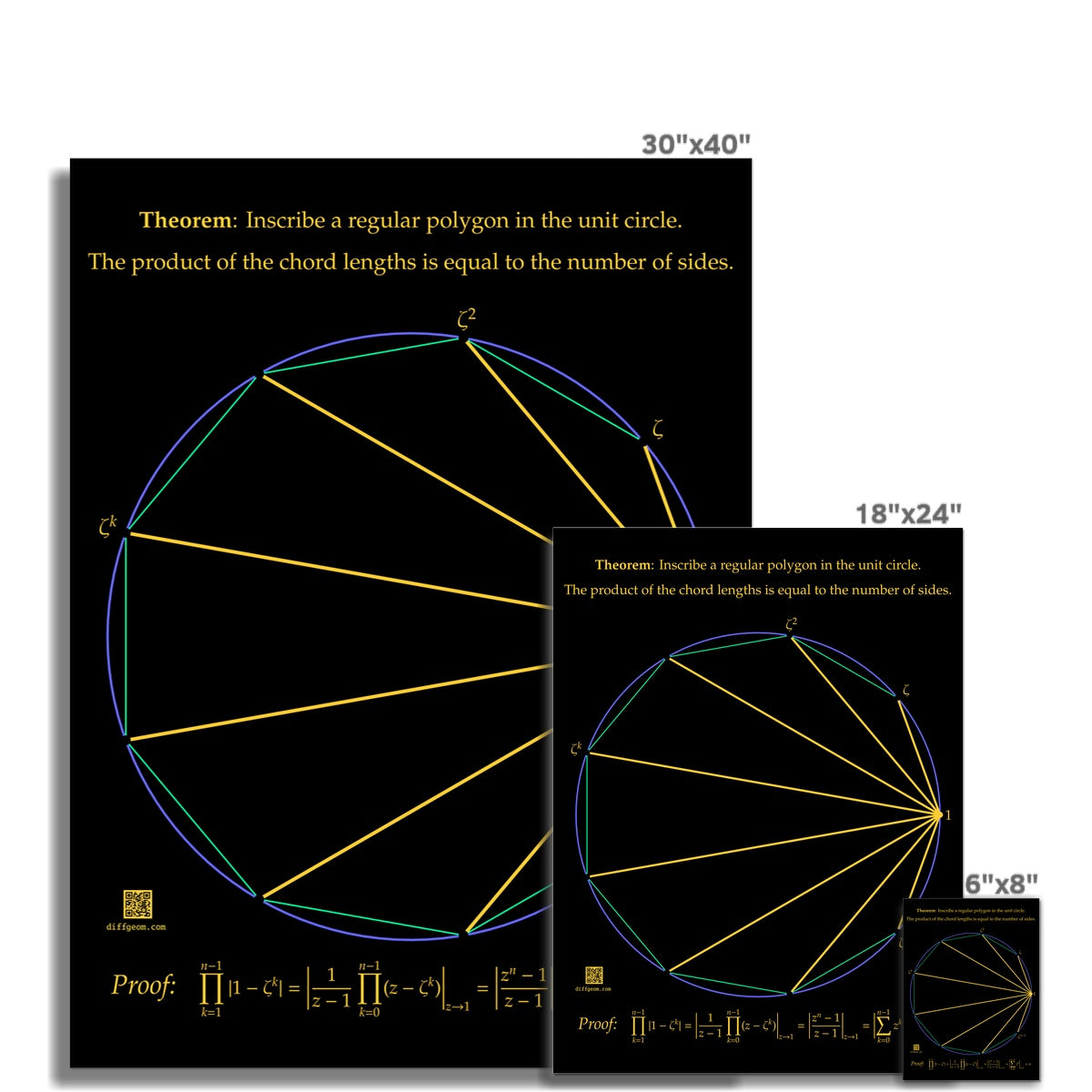
Product of Chord Lengths Fine Art Print
Product of Chord Lengths Fine Art Print
Regular price
$20.00 USD
Regular price
Sale price
$20.00 USD
Unit price
/
per
Shipping calculated at checkout.
Couldn't load pickup availability
Inscribe a regular