Projective Plane, Spring Fine Art Print

Take a rectangular strip of paper, make a half-twist, and attach the ends. The resulting surface, a Möbius strip, has a number of surprising properties. It is one-sided: If we attempt to color one side of the paper "continuing as far as we can" without lifting our pencil or brush, no uncolored paper remains when we finish. Cutting a Möbius strip along the center line yields a single twisted strip, not two linked strips.

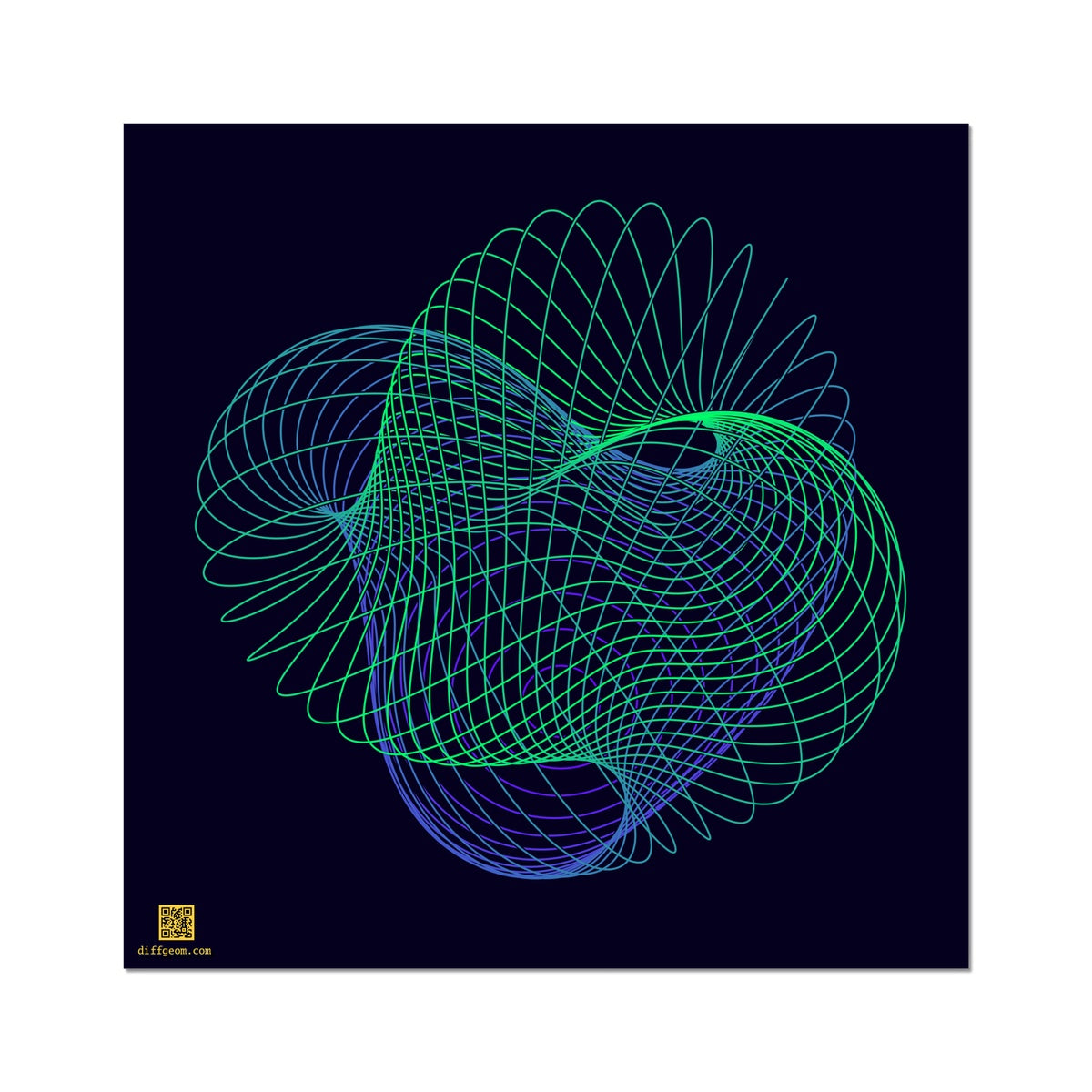
The boundary of a Möbius strip is a single closed loop, abstractly a circle. The boundary of a disk is also a circle. Abstractly, we can glue a Möbius strip to a disk, joining their circle boundaries and obtaining a one-sided surface with no boundary. To a topologist, this surface is the real projective plane. Boy's surface is a model of the real projective plane in Euclidean three-space.

Although Boy's surface "cuts through" itself, or has self-intersections, there is a unique tangent plane at each point of the abstract surface. With one exception, each point of three-space where the surface crosses itself corresponds to two points of the abstract surface; accordingly, two tangent planes to Boy's surface pass through most self-intersections. (There is a single "triple point" near the top center where three points of the abstract surface coincide.)

Abstractly, a point of Boy's surface may be viewed as representing a line through the origin in three-space. Since every such line meets the unit sphere in a pair of antipodes, Boy's surface is obtained from a sphere by gluing every point to its antipode.

The parametrization shown was published by Robert Bryant and Rob Kusner in 1986.

Printed on museum-quality fine art print paper (200 gsm) with a textured, matte finish.