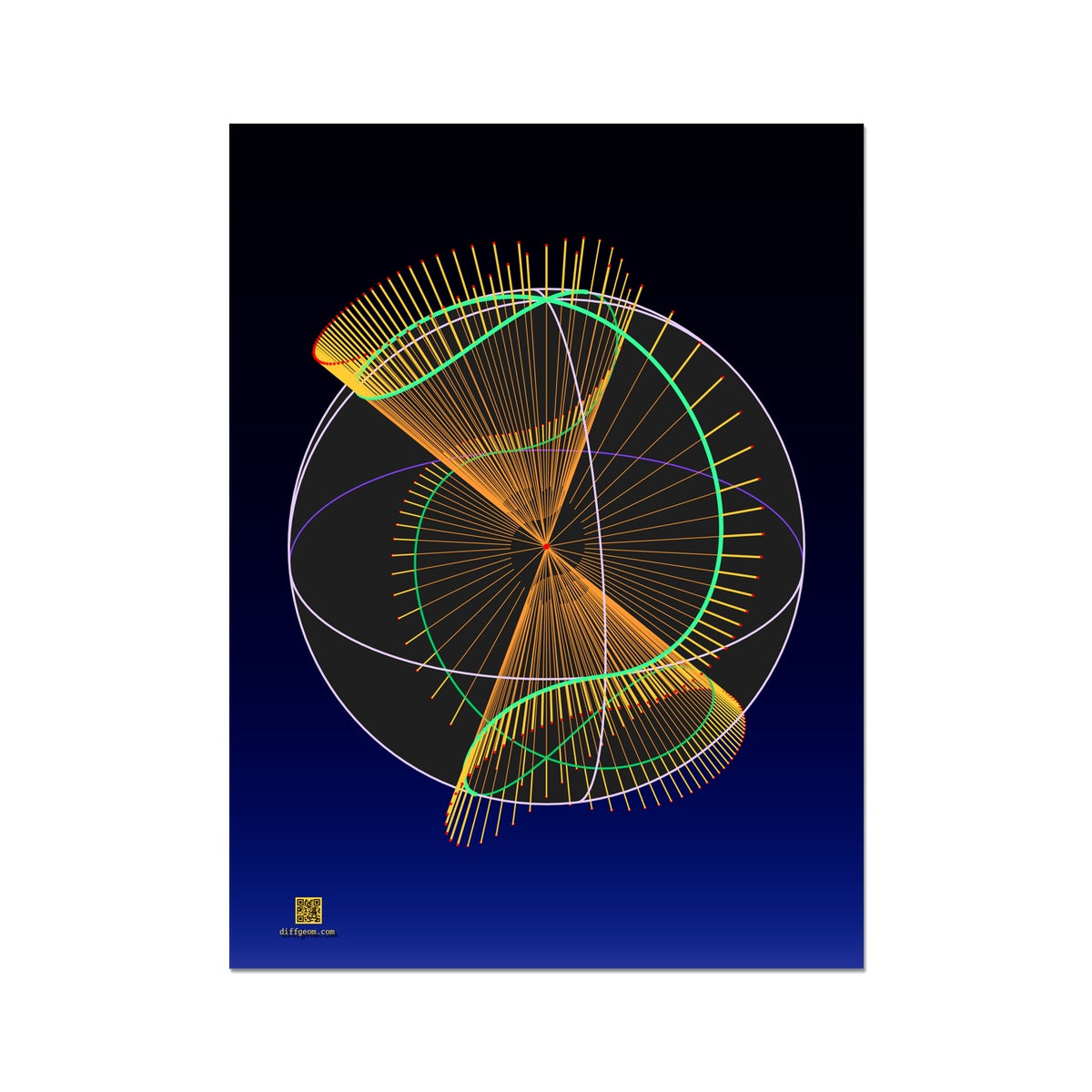
What does a curve in the \((x, y)\)-plane, such as a parabola or hyperbola, look like at infinity? The answer depends on what we mean by at infinity. One scheme is to place our curve in the projective plane: Identify the \((x, y)\)-plane with the plane \(z = 1\) in Cartesian three-space, and consider the cone comprising all lines through the origin and a point of our curve. Intersecting this cone with the planes \(x = 1\) or \(y = 1\) turns out to show our original curve with points at infinity!
The image shows the nodal cubic, whose equation is \(x^{3} - x^{2} + y^{2} = 0\), "projectivized" to a cone and intersected with the unit sphere.
Printed on museum-quality fine art print paper (200 gsm) with a textured, matte finish.
