Prodigi
Projective Line Wall Art Poster
Projective Line Wall Art Poster
Couldn't load pickup availability
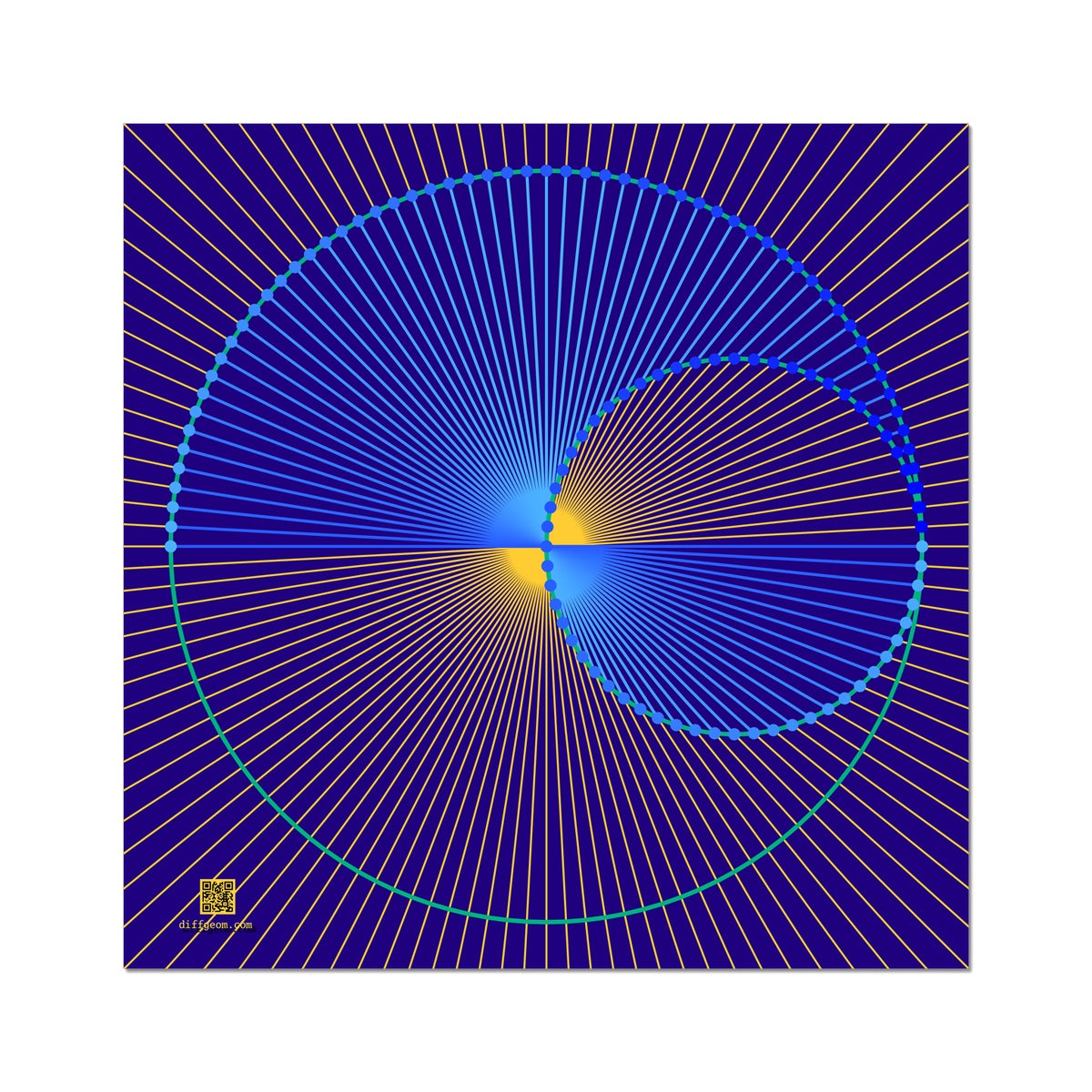
The "real projective line" is the set of lines through the origin in the Cartesian plane. If we consider the circle \(C\) of radius \(1/2\) centered at \((1/2, 0)\), each point on \(C\) corresponds to a unique line through the origin: The origin itself corresponds to the vertical axis (the tangent line at the origin), while every other point \(p\) is distinct from the origin and determines the line through the origin and \(p\). This gives two equivalent ways to view the projective line: As the circle \(C\), and as an ordinary number line with the value corresponding to the slope of a line, with one added point "at infinity" representing the vertical line, loosely of infinite slope.
In this picture, the circle of radius \(1\) about the origin is a "double covering" of \(C\): Each line through the origin corresponds to a pair of diametrically opposite points on the unit circle. The unit circle and \(C\) have polar equations \(r = 1\) and \(r = \cos\theta\). Both of these curves have unit speed; the double covering "evenly wraps" the unit circle around \(C\).
The same picture may be viewed as depicting all complex lines through the origin of the complex Cartesian plane, a real four-dimensional space. The complex projective line is the set of complex numbers with an added point at infinity. We may view the complex projective line as the "Riemann sphere" of complex analysis, or as the familiar real \(2\)-sphere by stereographic projection.
In the complex interpretation, the unit sphere is the three dimensional sphere in real four-space. Each complex line through the origin intersets the unit \(3\)-sphere in a great circle. The projection from the \(3\)-sphere to the complex projective line is known as the "Hopf map" or "Hopf fibration."
Printed on high-quality 170 gsm poster paper with a satin finish.
Share