Thomae's Function Wall Art Poster

Mathematical functions students encounter in calculus are usually given by a single formula, or sometimes finitely many formulas over different intervals.

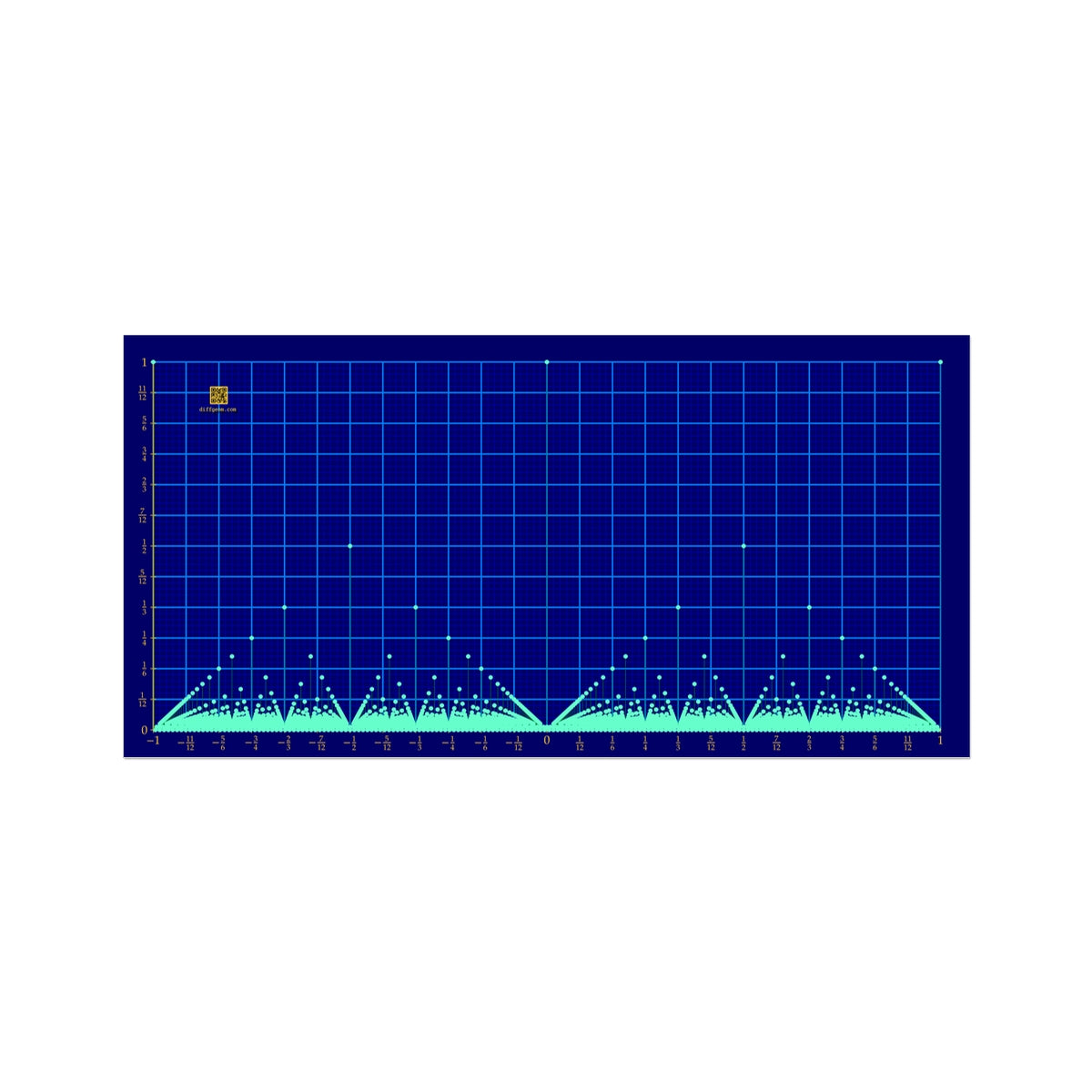
In real analysis, students see more "pathological" functions, such as Thomae's function. Thomae's function \(T\) accepts a real number \(x\) as input. If \(x\) is irrational, \(T(x) = 0\). If instead \(x = p/q\) is rational in lowest terms, \(T(x) = 1/q\).

This function has surprising properties that test students' facility with the definitions of real analysis. First, Thomae's function has limit equal to \(0\) at every real number. Consequently, Thomae's function is continuous at every irrational number and discontinuous at every rational. Despite having infinitely many discontinuities, however, Thomae's function is integrable over an arbitrary interval, and its integral is \(0\).

Printed on high-quality 170 gsm poster paper with a satin finish.