Uniform Convergence Wall Art Poster

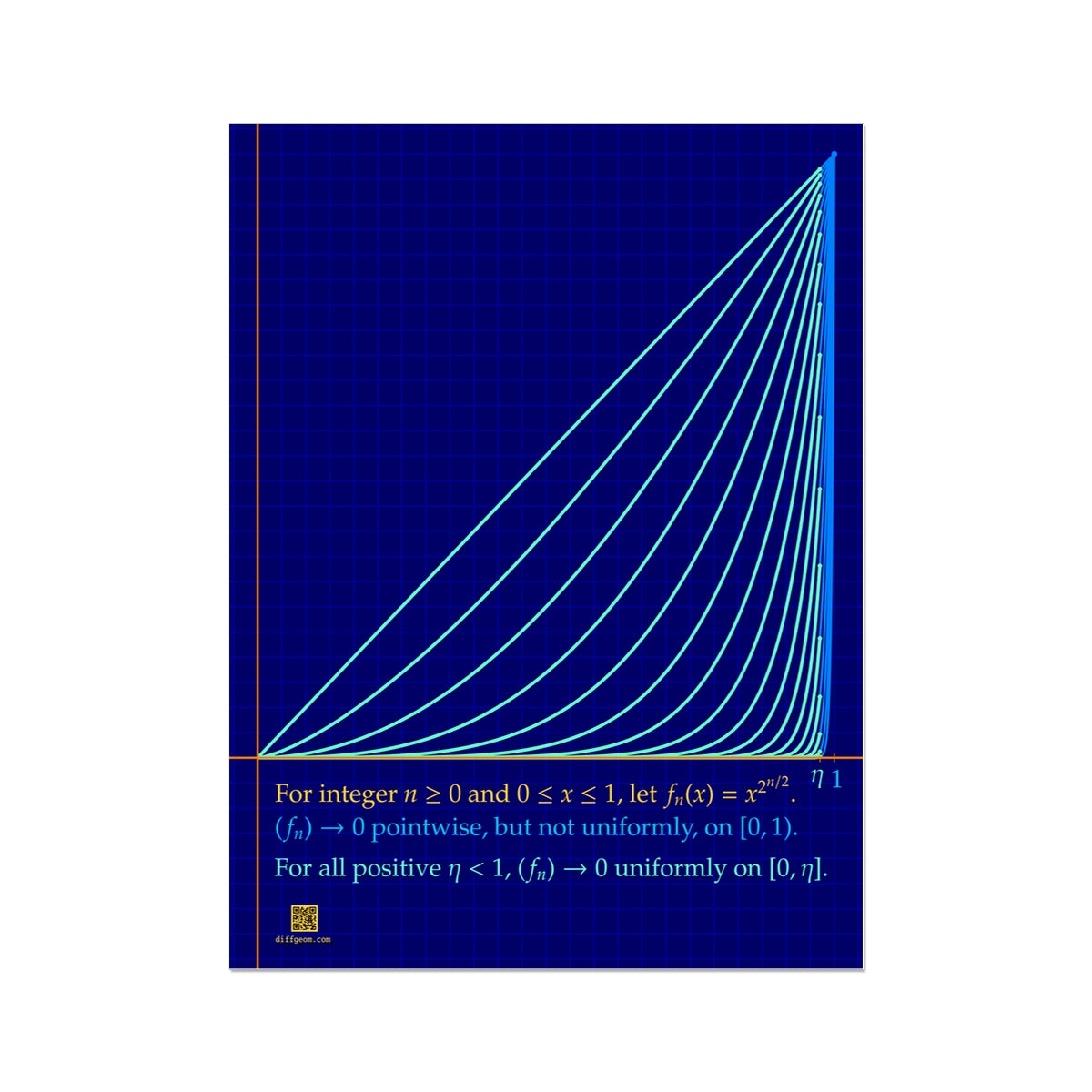
An early conceptual hurdle for students of analysis is convergence of sequences of numbers. A subsequent hurdle arises when we consider sequences of functions \((f_{n})\): There is more than one way a sequence of functions can converge!

Asked to define "convergence of a sequence of functions," many students would write down "pointwise" convergence of the numerical sequence \(\bigl(f_{n}(x)\bigr)\) for each \(x\) in the common domain of the \(f_{n}\). Unfortunately, a sequence of continuous functions may converge pointwise to a discontinuous limit. For example, if \(f_{n}(x) = x^{n}\), then each \(f_{n}\) is continuous on \([0, 1]\). On the other hand, \(f_{n}(x) \to 0\) if \(0 \leq x < 1\) while \(f_{n}(1) = 1 \to 1\); the limit function is discontinuous.

"Uniform convergence" on a domain is a stronger condition that more closely conforms to students' intuition. Unfortunately, distinguishing uniform convergence from pointwise convergence is technically subtle. This poster image depicts the difference visually in a prototypical example, essentially the functions \(f_{n}(x) = x^{n}\) for \(0 \leq x \leq 1\).

Printed on high-quality 170 gsm poster paper with a satin finish.